《機械》〈電気機器〉[H22:問7]低圧進相コンデンサに接続する直列リアクトルに関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

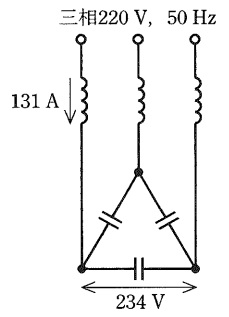
力率改善の目的で用いる低圧進相コンデンサは，図のように直列に\( \ 6 \ \mathrm {[％]} \ \)のリアクトルを接続することを標準としている。このため，回路電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)の設備に用いる進相コンデンサの定格電圧\( \ V_{\mathrm {N}} \ \mathrm {[V]} \ \)は，次の式で与えられる値となる。
\[
\begin{eqnarray}
V_{\mathrm {N}} &=&\frac {V_{\mathrm {L}}}{\displaystyle 1-\frac {L}{100}} \\[ 5pt ] \end{eqnarray}
\] ここで，\( \ L \ \)は，組み合わせて用いる直列リアクトルの\( \ ％ \ \)リアクタンスであり，\( \ L=6 \ \)である。

これから，回路電圧\( \ 220 \ \mathrm {[V]} \ \)（相電圧\( \ 127.0 \ \mathrm {[V]} \ \)）の三相受電設備に用いる進相コンデンサでは，コンデンサの定格電圧を\( \ 234 \ \mathrm {[V]} \ \)(相電圧\( \ 135.1 \ \mathrm {[V]} \ \))とする。

定格設備容量\( \ 50 \ \mathrm {[kvar]} \ \)，定格周波数\( \ 50 \ \mathrm {[Hz]} \ \)の進相コンデンサ設備を考える。その定格電流は，\( \ 131 \ \mathrm {[A]} \ \)となる。この進相コンデンサ設備に直列に接続するリアクトルのインダクタンス\( \ \mathrm {[mH]} \ \)（\( \ 1 \ \)相分）の値として，最も近いのは次のうちどれか。

　(1)　\( \ 0.20 \ \)　　(2)　\( \ 0.34 \ \)　　(3)　\( \ 3.09 \ \)　　(4)　\( \ 3.28 \ \)　　(5)　\( \ 5.35 \ \)　

【ワンポイント解説】

コンデンサ設備に接続するリアクトルのインダクタンスを導出する問題です。
解法自体は難しくありませんが，不要な数式や値が与えられていることから受験生が混乱する問題であったかもしれません。
問題文を読み解いてきちんと道筋を立てられるかを試される問題です。

1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
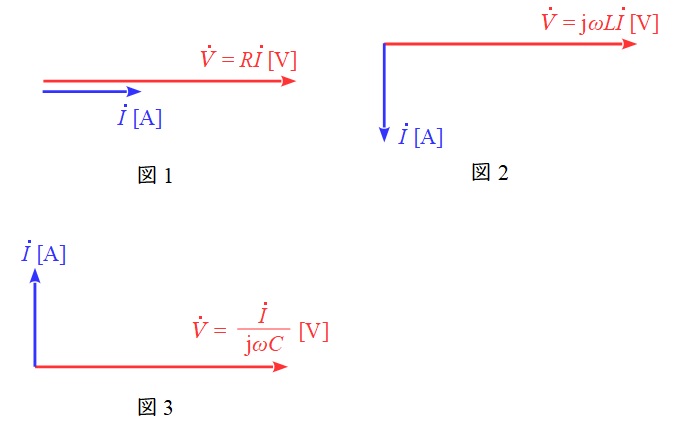
\] となります。この関係をベクトル図に表すと，図1～図3となります。

【解答】

解答：(1)
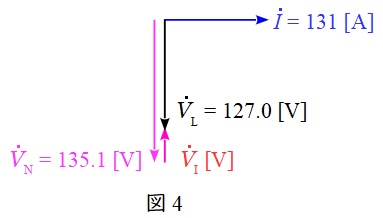
リアクトルにかかる電圧を\( \ {\dot V}_{\mathrm {I}} \ \mathrm {[V]} \ \)とし，題意に沿ってベクトル図を描くと図4のようになる。
図4より，リアクトルにかかる電圧\( \ V_{\mathrm {I}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {I}} &=&V_{\mathrm {N}}-V_{\mathrm {L}} \\[ 5pt ] &=&135.1-127.0 \\[ 5pt ] &=&8.1 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であり，周波数\( \ f=50 \ \mathrm {[Hz]} \ \)，定格電流\( \ I=131 \ \mathrm {[A]} \ \)であるから，\( \ 1 \ \)相分のインダクタンス\( \ L \ \mathrm {[mH]} \ \)は，ワンポイント解説「1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」の通り，
\[
\begin{eqnarray}
V_{\mathrm {I}}&=&2\pi f L I \\[ 5pt ] L&=&\frac {V_{\mathrm {I}}}{2\pi fI} \\[ 5pt ] &=&\frac {8.1}{2\pi \times 50 \times 131} \\[ 5pt ] &≒&0.000197 \ \mathrm {[H]}　→　0.20 \ \mathrm {[mH]} \\[ 5pt ] \end{eqnarray}
\] と求められる。