《機械》〈情報伝送及び処理〉[H24:問14]論理回路の論理式に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図のような論理回路において，入力\( \ A \ \)，\( \ B \ \)及び\( \ C \ \)に対する出力\( \ X \ \)の論理式，並びに入力を\( \ A=0 \ \)，\( \ B=1 \ \)，\( \ C=1 \ \)としたときの出力\( \ Y \ \)の値として，正しい組合せを次の(1)～(5)のうちから一つ選べ。

\[
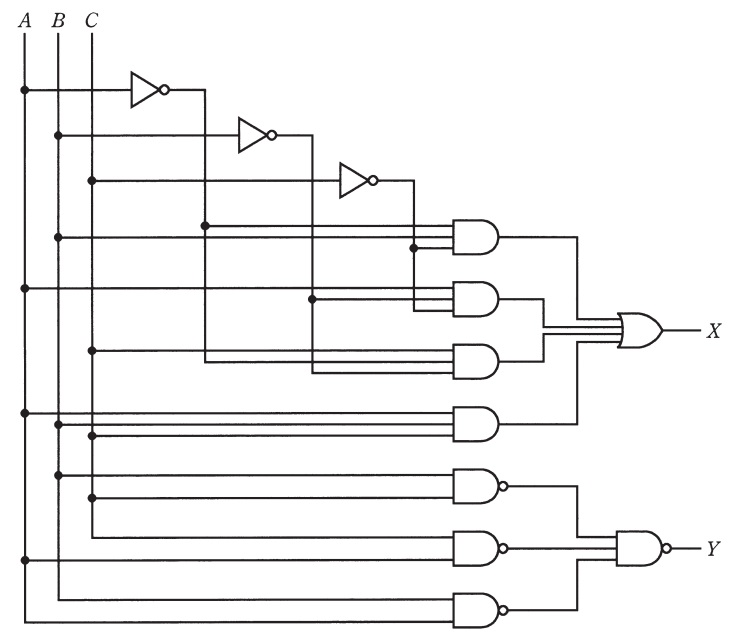
\begin{array}{cccc}
\hline
(1) & X=\overline A \cdot B \cdot \overline C+A\cdot \overline B \cdot \overline C+ \overline A \cdot \overline B \cdot C+ A \cdot B \cdot C & & Y=1 \\
\hline
(2) & X=\overline A \cdot B \cdot C+A\cdot \overline B \cdot \overline C+ \overline A \cdot \overline B \cdot C+ A \cdot B \cdot C & & Y=0 \\
\hline
(3) & X=\overline A \cdot B \cdot C+A\cdot \overline B \cdot \overline C+ \overline A \cdot \overline B \cdot C+ A \cdot B \cdot \overline C & & Y=1 \\
\hline
(4) & X=\overline A \cdot B \cdot \overline C+A\cdot \overline B \cdot \overline C+ \overline A \cdot \overline B \cdot C+ A \cdot B \cdot C & & Y=0 \\
\hline
(5) & X=\overline A \cdot B \cdot C+\overline A\cdot B \cdot C+ \overline A \cdot \overline B \cdot \overline C+ A \cdot B \cdot C & & Y=1 \\
\hline
\end{array}
\]

【ワンポイント解説】

演習としてはじっくりと取り組んで頂いて構わない問題ですが，試験本番では遅くても10分以内に解く必要があります。解き方のコツ等本問で理解するようにしましょう。

1.主な論理回路の真理値表
\( \ \mathrm {AND} \ \)回路はすべての入力が\( \ 1 \ \)の時のみ\( \ 1 \ \)が出力される回路で，\( \ \mathrm {OR} \ \)回路は入力が一つでも\( \ 1 \ \)の時\( \ 1 \ \)が出力される回路です。その他，以下の真理値表は知っておきましょう。

　表1　\( \ \mathrm {AND} \ \)回路
\[
\begin{array}{ccc|c}
A & B & C & 出力 \\
\hline
0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 1 & 1 & 0 \\
1 & 0 & 0 & 0 \\
1 & 0 & 1 & 0 \\
1 & 1 & 0 & 0 \\
1 & 1 & 1 & 1 \\
\end{array}
\]

　表2　\( \ \mathrm {OR} \ \)回路
\[
\begin{array}{ccc|c}
A & B & C & 出力 \\
\hline
0 & 0 & 0 & 0 \\
0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 \\
0 & 1 & 1 & 1 \\
1 & 0 & 0 & 1 \\
1 & 0 & 1 & 1 \\
1 & 1 & 0 & 1 \\
1 & 1 & 1 & 1 \\
\end{array}
\]

　表3　\( \ \mathrm {NOT} \ \)回路
\[
\begin{array}{c|c}
A & 出力 \\
\hline
0 & 1 \\
1 & 0 \\
\end{array}
\]

　表4　\( \ \mathrm {NAND} \ \)回路
\[
\begin{array}{ccc|c}
A & B & C & 出力 \\
\hline
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 \\
0 & 1 & 1 & 1 \\
1 & 0 & 0 & 1 \\
1 & 0 & 1 & 1 \\
1 & 1 & 0 & 1 \\
1 & 1 & 1 & 0 \\
\end{array}
\]

　表5　\( \ \mathrm {NOR} \ \)回路
\[
\begin{array}{ccc|c}
A & B & C & 出力 \\
\hline
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 1 & 1 & 0 \\
1 & 0 & 0 & 0 \\
1 & 0 & 1 & 0 \\
1 & 1 & 0 & 0 \\
1 & 1 & 1 & 0 \\
\end{array}
\]

【解答】

解答：(1)
出力\( \ X \ \)にかかる各記号と信号の変化について図1に示す。

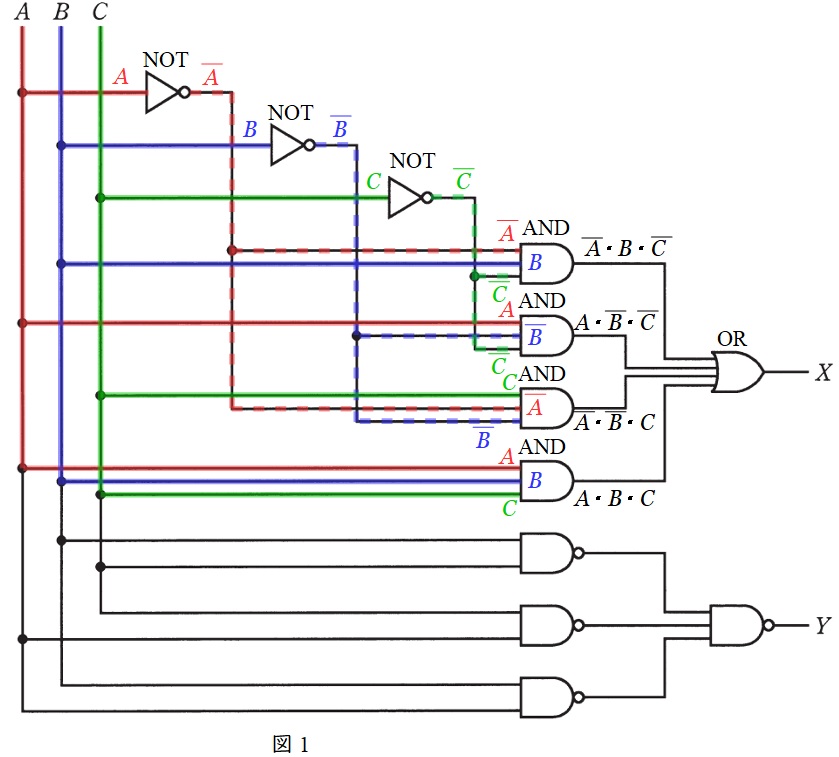
図1より，出力される\( \ X \ \)は，
\[
\begin{eqnarray}
X&=&\overline A \cdot B \cdot \overline C+A\cdot \overline B \cdot \overline C+ \overline A \cdot \overline B \cdot C+ A \cdot B \cdot C \\[ 5pt ] \end{eqnarray}
\] と求められる。
出力\( \ Y \ \)にかかる各記号と信号の変化について図2に示す。

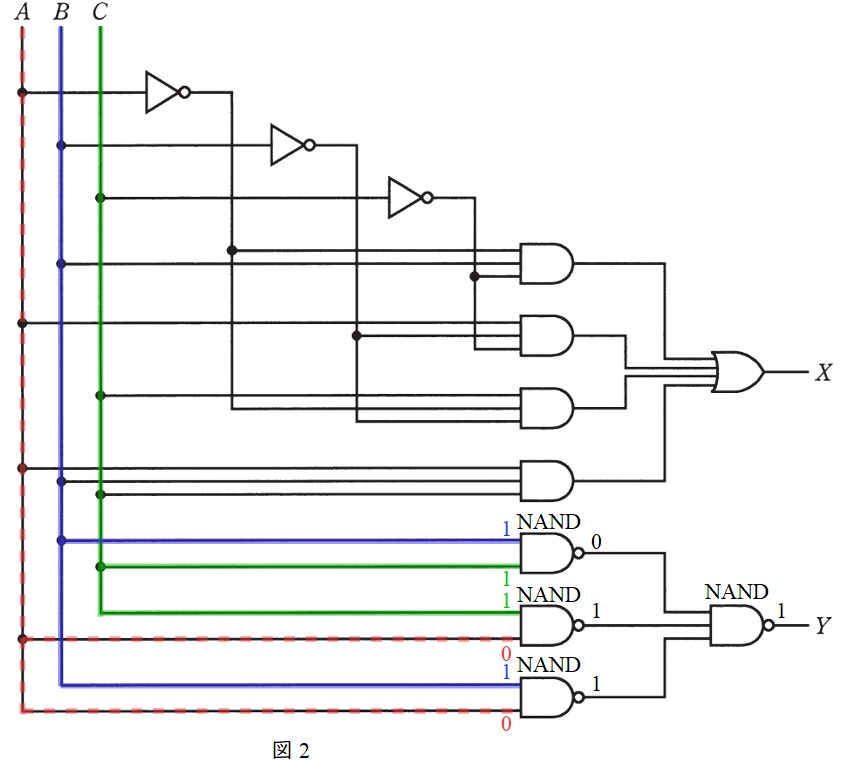
図2より，出力される\( \ Y \ \)は，
\[
\begin{eqnarray}
Y&=&1 \\[ 5pt ] \end{eqnarray}
\] と求められる。