《機械》〈回転機〉[H26:問15]三相同期電動機(星形結線)に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

周波数が\( \ 60 \ \mathrm {Hz} \ \)の電源で駆動されている4極の三相同期電動機(星形結線)があり，端子の相電圧\( \ V \ \mathrm {[V]} \ \)は\( \ \displaystyle \frac {400}{\sqrt {3}} \ \mathrm {V} \ \)，電機子電流\( \ I_{\mathrm {M}} \ \mathrm {[A]} \ \)は\( \ 200 \ \mathrm {A} \ \)，力率\( \ 1 \ \)で運転している。1相の同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)は\( \ 1.00 \ \mathrm {\Omega } \ \)であり，電機子の巻線抵抗，及び機械損などの損失は無視できるものとして，次の(a)及び(b)の問に答えよ。

(a)　上記の同期電動機のトルクの値\( \ \mathrm {[N\cdot m]} \ \)として最も近いものを，次の(1)～(5)のうちから一つ選べ。

　(1)　12.3　　(2)　368　　(3)　735　　(4)　1270　　(5)　1470

(b)　上記の同期電動機の端子電圧及び出力を一定にしたまま界磁電流を増やしたところ，電機子電流が\(I_{\mathrm {M1}} \ \mathrm {[A]}\)に変化し，力率\(\cos \theta \)が\(\displaystyle \frac {\sqrt {3}}{2} \ ( \theta =30°) \)の進み負荷となった。出力が一定なので入力電力は変わらない。図はこのときの状態を説明するための1相の概略のベクトル図である。このときの1相の誘導起電力\(E \ \mathrm {[V]}\)として，最も近い\(E\)の値を次の(1)～(5)のうちから一つ選べ。

　　

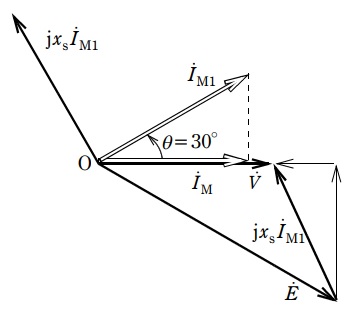
　(1)　374　　(2)　387　　(3)　400　　(4)　446　　(5)　475

【ワンポイント解説】

同期電動機の特性に関する問題で，等価回路を描いて回路方程式を立てることとベクトル図を描いて幾何計算をすることがもとめられます。(b)のベクトル図がヒントとなっているので確実に解けるようにしましょう。

1.同期電動機の等価回路
同期電動機の一相分の等価回路は図1のようになります。ここで\( \ \dot V \ \)は端子電圧，\( \ \dot E \ \)は誘導起電力，\( \ {\dot I}_{\mathrm {M}} \ \)は電機子電流，\( \ {\dot I}_{0} \ \)は励磁電流，\(x_{\mathrm {s}} \ \)は同期リアクタンスとなります。

2.同期電動機の出力\( \ P \ \)とトルク\( \ T \ \)
図1で与えられる電動機が回転数\( \ N \ \mathrm {[{min}^{-1}]} \ \)で運転している同期電動機の出力\( \ P \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P &=&3VI_{\mathrm {M}}\cos \theta \\[ 5pt ] &=&\frac {3EV}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] \end{eqnarray}
\] となり，同期電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T &=&\frac {P}{\omega } \\[ 5pt ] &=&\frac {P}{\displaystyle \frac {2\pi N}{60}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.電動機の同期速度\( \ N_{\mathrm {s}} \ \)
電源周波数\( \ f \ \mathrm {[Hz]} \ \)と極数\( \ p \ \)が与えられている時同期速度\( \ N_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(3)
図1の等価回路より，
\[
\dot V=\dot E+\mathrm {j}x_{\mathrm {s}}{\dot I}_{\mathrm {M}}
\] であり，力率が1であるから，題意に沿ってベクトル図を描くと図2のようになる。

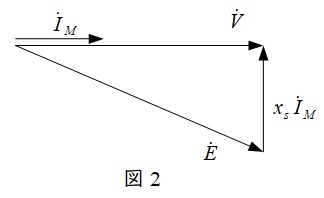
ワンポイント解説「2.同期電動機の出力\( \ P \ \)とトルク\( \ T \ \)」より出力\( \ P \ \)は，
\[
\begin{eqnarray}
P &=&3VI_{\mathrm {M}}\cos \theta \\[ 5pt ] &=&3\times \frac {400}{\sqrt {3}}\times 200\times 1 \\[ 5pt ] &=&\frac {240000}{\sqrt {3}} \\[ 5pt ] \end{eqnarray}
\] となる。また，ワンポイント解説「3.電動機の同期速度\( \ N_{\mathrm {s}} \ \)」より，電動機の回転速度\( \ N \ \)は，
\[
\begin{eqnarray}
N &=&\frac {120f}{p} \\[ 5pt ] &=&\frac {120\times 60}{4} \\[ 5pt ] &=&1800 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] となるので，トルク\( \ T \ \)は，
\[
\begin{eqnarray}
T &=&\frac {P}{\omega } \\[ 5pt ] &=&\frac {P}{\displaystyle \frac {2\pi N}{60}} \\[ 5pt ] &=&\frac {\displaystyle \frac {240000}{\sqrt {3}}}{\displaystyle \frac {2\pi \times 1800}{60}} \\[ 5pt ] &≒&735.1　→　735 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
問題図より，\( \ {\dot I}_{\mathrm {M1}} \ \)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {M1}} &=&I_{\mathrm {M}}\times \frac {2}{\sqrt {3}} \\[ 5pt ] &=&200\times \frac {2}{\sqrt {3}}\\[ 5pt ] &=&\frac {400}{\sqrt {3}} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，\( \ x_{\mathrm {s}} \ \)での電圧降下の大きさは，
\[
\begin{eqnarray}
x_{\mathrm {s}}I_{\mathrm {M1}} &=&1\times \frac {400}{\sqrt {3}} \\[ 5pt ] &=&\frac {400}{\sqrt {3}} \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\( \ x_{\mathrm {s}}{\dot I}_{\mathrm {M1}} \ \)の実軸成分と虚軸成分の大きさはそれぞれ，
\[
\begin{eqnarray}
\left( x_{\mathrm {s}}{\dot I}_{\mathrm {M1}}\right) _{\mathrm {Re}} &=&\frac {400}{\sqrt {3}}\sin 30° \\[ 5pt ] &=&\frac {200}{\sqrt {3}} \ \mathrm {[V]} \\[ 5pt ] \left( x_{\mathrm {s}}{\dot I}_{\mathrm {M1}}\right) _{\mathrm {Im}} &=&\frac {400}{\sqrt {3}}\cos 30° \\[ 5pt ] &=&200 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
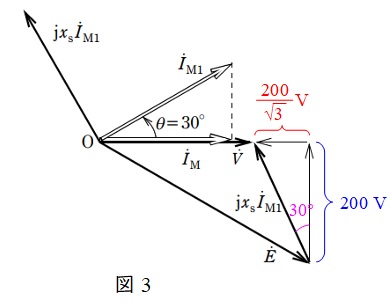
\] となるので，各部の大きさは図3のように整理でき，電圧\( \ \dot E \ \)の大きさは，
\[
\begin{eqnarray}
E &=&\sqrt {\left( V+\frac {200}{\sqrt {3}}\right) ^{2}+200^{2}} \\[ 5pt ] &=&\sqrt {\left( \frac {400}{\sqrt {3}}+\frac {200}{\sqrt {3}}\right) ^{2}+200^{2}} \\[ 5pt ] &=&400 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。