《機械》〈情報伝送及び処理〉[R01:問14]2進数の演算に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

\( \ 2 \ \)進数\( \ A \ \)と\( \ B \ \)がある。それらの和が\( \ A+B=\left( 101010\right) _{2} \ \)，差が\( \ A-B=\left( 1100\right) _{2} \ \)であるとき，\( \ B \ \)の値として，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ \left( 1110 \right) _{2} \ \)　　(2)　\( \ \left( 1111 \right) _{2} \ \)　　(3)　\( \ \left( 10011 \right) _{2} \ \)　　(4)　\( \ \left( 10101 \right) _{2} \ \)　　(5)　\( \ \left( 11110 \right) _{2} \ \)

【ワンポイント解説】

直接計算する方法、\( \ 10 \ \)進数に変換してから解く方法等様々な解法が考えられます。どのやり方でも正答が出れば問題ありません。

【解答】

解答：(2)
題意より\( \ B \ \)を導出するため，\( \ A+B \ \)から\( \ A-B \ \)を引くと，
\[
\begin{array}{ccccccccc}
& A+B & = & 1 & 0 & 1 & 0 & 1 & 0 \\
-) & A-B & = & 0 & 0 & 1 & 1 & 0 & 0 \\
\hline
& 2B & = & 0 & 1 & 1 & 1 & 1 & 0 \\
\end{array}
\] となるので，両辺\( \ 2 \ \)で割ると，右辺は一桁下がるので，
\[
\begin{array}{ccccccccc}
& B & = & 0 & 0 & 1 & 1 & 1 & 1 \\
\end{array}
\] となり，解答は\( \ \left( 1111 \right) _{2} \ \)と求められる。

[別解]
\( \ 2 \ \)進数を\( \ 10 \ \)進数にするためには各桁に\( \ 2^{x}(x=0,1,2・・・) \ \)乗をかけて導出する。本問においては，
\[
\begin{eqnarray}
A+B &=&\left( 101010\right) _{2} \\[ 5pt ] &=&1\times 2^{5}+0\times 2^{4}+1\times 2^{3}+0\times 2^{2}+1\times 2^{1}+0\times 2^{0} \\[ 5pt ] &=&32+0+8+0+2+0 \\[ 5pt ] &=&42 　・・・・・・・・・・・・・　① \\[ 5pt ] A-B &=&\left( 1100\right) _{2} \\[ 5pt ] &=&1\times 2^{3}+1\times 2^{2}+0\times 2^{1}+0\times 2^{0} \\[ 5pt ] &=&8+4+0+0 \\[ 5pt ] &=&12 　・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となり，\( \ ①-② \ \)より，
\[
\begin{eqnarray}
2B &=&30 \\[ 5pt ] B&=&15 \\[ 5pt ] \end{eqnarray}
\] と求められる。\( \ 10 \ \)進数を\( \ 2 \ \)進数にするためには，\( \ 10 \ \)進数を\( \ 2 \ \)で割っていき，その余りの数を下から並べると求められるので，

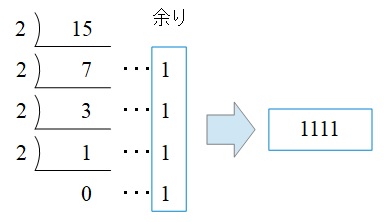
となり，解答は\( \ \left( 1111 \right) _{2} \ \)となる。