《機械》〈自動制御〉[R4下:問15]周波数伝達関数とボード線図に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図は，抵抗，インダクタンス，キャパシタンスで構成された\( \ \mathrm {RLC} \ \)回路である。次の(a)及び(b)の問に答えよ。

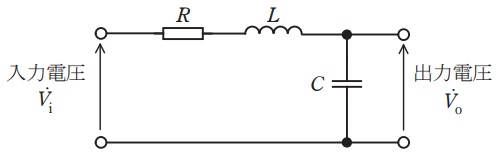
(a)　図において，入力電圧\( \ {\dot V}_{\mathrm {i}} \ \)に対する出力電圧\( \ {\dot V}_{\mathrm {o}} \ \)の伝達関数\( \ G\left( \mathrm {j}\omega \right) ( =\displaystyle \frac {{\dot V}_{\mathrm {o}}}{{\dot V}_{\mathrm {i}}}) \ \)を求め，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ \displaystyle \frac {1}{1+\omega ^{2}LC+\mathrm {j}\omega CR} \ \)　　　(2)　\( \ \displaystyle \frac {1}{1-\omega ^{2}LC+\mathrm {j}\omega CR} \ \)

　(3)　\( \ \displaystyle \frac {\sqrt {LC}}{1+\omega ^{2}LC+\mathrm {j}\omega CR} \ \)　　　(4)　\( \ \displaystyle \frac {\sqrt {LC}}{1-\omega ^{2}LC+\mathrm {j}\omega CR} \ \)

　(5)　\( \ \displaystyle \frac {\omega ^{2}LC}{\omega ^{2}LC-1-\mathrm {j}\omega CR} \ \)

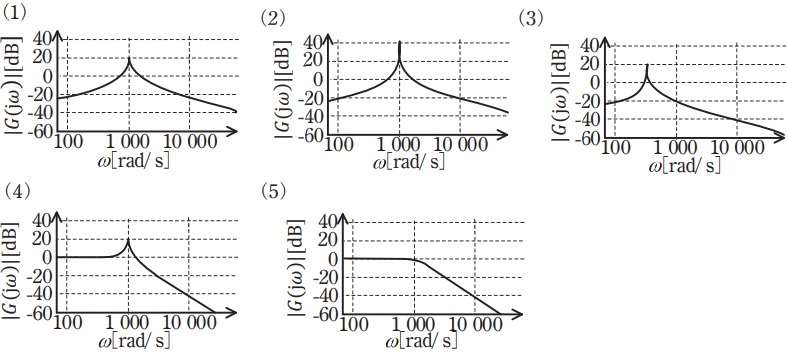
(b)　図において，\( \ R=1 \ \mathrm {\Omega } \ \)，\( \ L=0.01 \ \mathrm {H} \ \)，\( \ C=100 \ \mathrm {\mu F} \ \)とした場合，(a)で求めた伝達関数を表すボード線図（ゲイン特性図）として，最も近いものを次の(1)～(5)のうちから一つ選べ。

【ワンポイント解説】

電気回路から周波数伝達関数を求め，そこからボード線図を導出する問題です。
(a)はできれば得点しておきたいですが，(b)はやや計算量が多く，正答率が低めであると予想されることから，正答できれば計算力は十分に自信を持って良いレベルと考えて良いかと思います。

1.ボード線図
周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {K}{1+\mathrm {j}\omega T} \ \)で与えられる時，ゲイン\( \ g \ \)は，
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ] &=&20\log _{10} \frac {K}{\sqrt {1+\left( \omega T\right) ^{2}}} \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] となりますが，\( \ \displaystyle \omega \ll \frac {1}{T} \ \)すなわち\( \ \omega T \ll 1 \ \)のとき，
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {1+0}} \\[ 5pt ] &=&20\log _{10}K \\[ 5pt ] \end{eqnarray}
\] とほぼ一定の値となり，\( \ \displaystyle \omega \gg \frac {1}{T} \ \)すなわち\( \ \omega T \gg 1 \ \)のとき，
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {\left( \omega T\right) ^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {K}{\omega T} \\[ 5pt ] &=&20\log _{10} K-20\log _{10}\omega T \\[ 5pt ] \end{eqnarray}
\] となり，横軸に対数座標をとると，ほぼ直線的に減少していくことになります。したがって，ボード線図は図1のようになります。
図1において\( \ \displaystyle \omega =\frac {1}{T} \ \)となる角周波数を折れ点角周波数と呼びます。

【解答】

(a)解答：(2)
分圧の法則より，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {o}}&=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C}}{R+\mathrm {j}\omega L+\displaystyle \frac {1}{\mathrm {j}\omega C}}{\dot V}_{\mathrm {i}} \\[ 5pt ] \frac {{\dot V}_{\mathrm {o}}}{{\dot V}_{\mathrm {i}}}&=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C}}{R+\mathrm {j}\omega L+\displaystyle \frac {1}{\mathrm {j}\omega C}} \\[ 5pt ] &=&\frac {1}{\mathrm {j}\omega CR+\mathrm {j}\omega C\cdot \mathrm {j}\omega L+1} \\[ 5pt ] &=&\frac {1}{\mathrm {j}\omega CR-\omega C\cdot \omega L+1} \\[ 5pt ] &=&\frac {1}{1-\omega ^{2}LC+\mathrm {j}\omega CR} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
(a)の解答式のゲイン\( \ g \ \mathrm {[dB]} \ \)は，ワンポイント解説「1.ボード線図」の通り，
\[
\begin{eqnarray}
g&=&20\log _{10} \left| G(\mathrm {j}\omega )\right| \\[ 5pt ] &=&20\log _{10} \frac {1}{\sqrt {\left( 1-\omega ^{2}LC\right) ^{2}+\left( \omega CR\right) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
g&=&20\log _{10} \frac {1}{\sqrt {\left( 1-\omega ^{2}\times 0.01\times 100\times 10^{-6}\right) ^{2}+\left( \omega \times 100\times 10^{-6}\times 1\right) ^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {1}{\sqrt {\left( 1-1\times 10^{-6}\omega ^{2}\right) ^{2}+\left( 1\times 10^{-4}\omega \right) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] となる。上式に\( \ \omega =100 \ \mathrm {[rad / s]} \ \)を代入すると，
\[
\begin{eqnarray}
g&=&20\log _{10} \frac {1}{\sqrt {\left( 1-1\times 10^{-6}\times 100 ^{2}\right) ^{2}+\left( 1\times 10^{-4}\times 100 \right) ^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {1}{\sqrt {\left( 1-1\times 10^{-2}\right) ^{2}+\left( 1\times 10^{-2} \right) ^{2}}} \\[ 5pt ] &≒&20\log _{10} \frac {1}{\sqrt {1+\left( 1\times 10^{-2} \right) ^{2}}} \\[ 5pt ] &≒&20\log _{10} \frac {1}{\sqrt {1}} \\[ 5pt ] &≒&20\log _{10} 1 \\[ 5pt ] &≒&0 \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \omega =1 \ 000 \ \mathrm {[rad / s]} \ \)を代入すると，
\[
\begin{eqnarray}
g&=&20\log _{10} \frac {1}{\sqrt {\left( 1-1\times 10^{-6}\times 1 \ 000 ^{2}\right) ^{2}+\left( 1\times 10^{-4}\times 1 \ 000 \right) ^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {1}{\sqrt {\left( 1-1\right) ^{2}+\left( 1\times 10^{-1} \right) ^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {1}{\sqrt {\left( 1\times 10^{-1} \right) ^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {1}{1\times 10^{-1}} \\[ 5pt ] &=&20\log _{10} 10 \\[ 5pt ] &=&20 \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \omega =10 \ 000 \ \mathrm {[rad / s]} \ \)を代入すると，
\[
\begin{eqnarray}
g&=&20\log _{10} \frac {1}{\sqrt {\left( 1-1\times 10^{-6}\times 10 \ 000 ^{2}\right) ^{2}+\left( 1\times 10^{-4}\times 10 \ 000 \right) ^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {1}{\sqrt {\left( 1-1\times 10^{2}\right) ^{2}+1 ^{2}}} \\[ 5pt ] &≒&20\log _{10} \frac {1}{\sqrt {\left( -1\times 10^{2}\right) ^{2}+1}} \\[ 5pt ] &=&20\log _{10} \frac {1}{\sqrt {1\times 10^{4}+1}} \\[ 5pt ] &≒&20\log _{10} \frac {1}{\sqrt {1\times 10^{4}}} \\[ 5pt ] &≒&20\log _{10} \frac {1}{1\times 10^{2}} \\[ 5pt ] &≒&20\log _{10} \left( 1\times 10^{-2}\right) \\[ 5pt ] &≒&-40 \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，条件を満たすグラフは(4)と求められる。