《機械》〈自動制御〉[R05下:問13]フィードバック制御系のボード線図に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

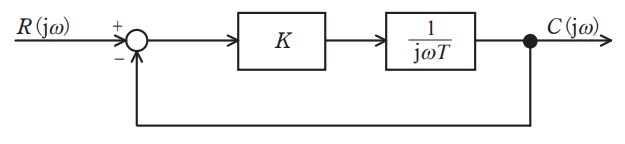
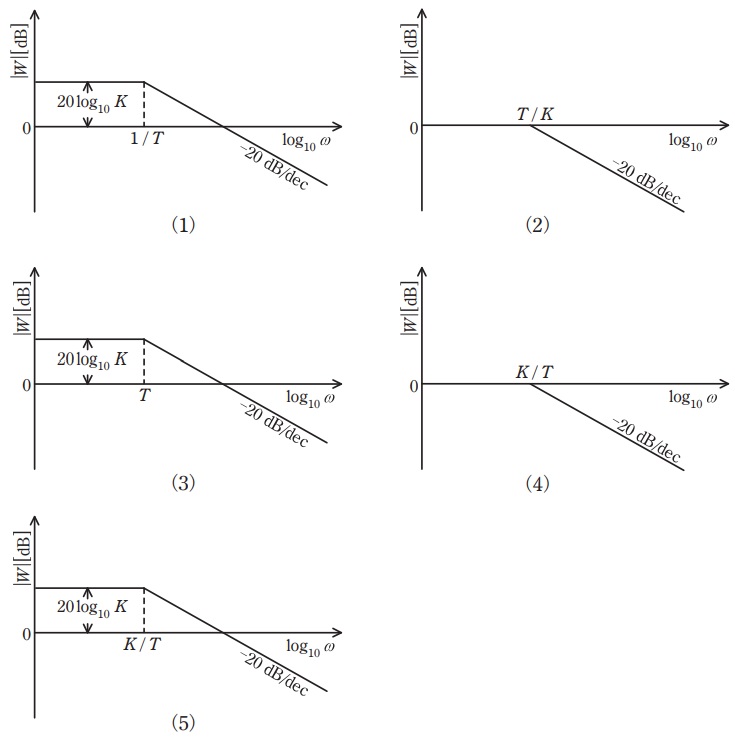
図に示すようなフィードバック制御系がある。閉ループ周波数伝達関数\( \ \displaystyle W \left( \mathrm {j}\omega \right) =\frac {C \left( \mathrm {j}\omega \right) }{R \left( \mathrm {j}\omega \right) } \ \)のボード線図の折線近似ゲイン特性として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，\( \ \omega \ \)は角周波数\( \ \mathrm {[rad / s]} \ \)を表す。

【ワンポイント解説】

ブロック線図から周波数伝達関数を求めボート線図を選択する問題です。
ブロック線図の計算だけでも一つの問題，周波数伝達関数からボード線図を選定するだけでも一つの問題となり得る内容なので，しっかりと学習が進んでいる受験生でないと正答は導けないかもしれません。
本問はやや古いですが，平成7年問13からの再出題となります

1.ブロック線図の考え方
①直列
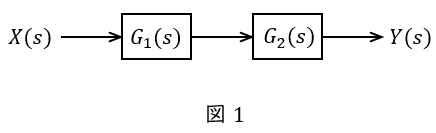
図1のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
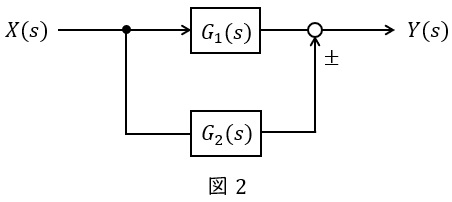
図2のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ] \end{eqnarray}
\] となります。

③フィードバック
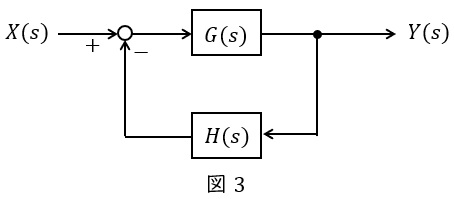
図3のような\( \ G(s) \ \)，\( \ H(s) \ \)が与えられているとき，全体の伝達関数\( \ W(s) \ \)は，
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ] Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ] Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ] \left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ] \frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ] W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ] \end{eqnarray}
\] となります。

2.ボード線図
周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {K}{1+\mathrm {j}\omega T} \ \)で与えられる時，ゲイン\( \ g \ \mathrm {[dB]} \ \)は，
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ] &=&20\log _{10} \frac {K}{\sqrt {1+\left( \omega T\right) ^{2}}} \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] となりますが，\( \ \displaystyle \omega \ll \frac {1}{T} \ \)すなわち\( \ \omega T \ll 1 \ \)のとき，
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {1+0}} \\[ 5pt ] &=&20\log _{10}K \\[ 5pt ] \end{eqnarray}
\] とほぼ一定の値となり，\( \ \displaystyle \omega \gg \frac {1}{T} \ \)すなわち\( \ \omega T \gg 1 \ \)のとき，
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {\left( \omega T\right) ^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {K}{\omega T} \\[ 5pt ] &=&20\log _{10} K-20\log _{10}\omega T \\[ 5pt ] \end{eqnarray}
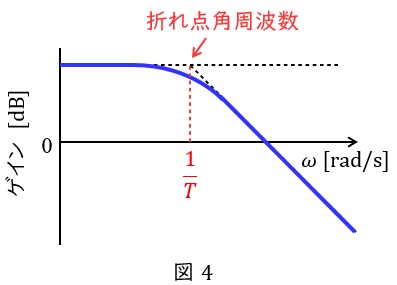
\] となり，横軸に対数座標をとると，ほぼ直線的に減少していくことになります。したがって，ボード線図は図4のようになります。
図4において\( \ \displaystyle \omega =\frac {1}{T} \ \)となる角周波数を折れ点角周波数と呼びます。

【解答】

解答：(4)
問題図のフィードバック制御系はワンポイント解説「1.ブロック線図の考え方　③フィードバック」の式に\( \ \displaystyle G\left( \mathrm {j}\omega \right) =K\cdot \frac {1}{\mathrm {j}\omega T} \ \)及び\( \ H\left( \mathrm {j}\omega \right) =1 \ \)を代入したものであるから，
\[
\begin{eqnarray}
W\left( \mathrm {j}\omega \right) &=&\frac {\displaystyle K\cdot \frac {1}{\mathrm {j}\omega T}}{\displaystyle 1+K\cdot \frac {1}{\mathrm {j}\omega T}\cdot 1} \\[ 5pt ] &=&\frac {\displaystyle \frac {K}{\mathrm {j}\omega T}}{\displaystyle \frac {K+\mathrm {j}\omega T}{\mathrm {j}\omega T}} \\[ 5pt ] &=&\frac {K}{K+\mathrm {j}\omega T} \\[ 5pt ] \end{eqnarray}
\] となるので，この関数のゲイン\( \ g \ \mathrm {[dB]} \ \)は，ワンポイント解説「2.ボード線図」の通り，
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ] &=&20\log _{10} \frac {K}{\sqrt {K^{2}+\left( \omega T\right) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] となる。\( \ \omega \ \mathrm {[rad / s]} \ \)が十分に小さい時，
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {K^{2}}} \\[ 5pt ] &=&20\log _{10} 1 \\[ 5pt ] &=&0 \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \omega \ \mathrm {[rad / s]} \ \)が十分に大きい時，
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {\left( \omega T\right) ^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {K}{\omega T} \\[ 5pt ] &=&20\log _{10} K-20\log _{10} \omega T \\[ 5pt ] \end{eqnarray}
\] となる。上式においてゲイン\( \ g=0 \ \mathrm {[dB]} \ \)となる\( \ \omega \ \mathrm {[rad / s]} \ \)は，
\[
\begin{eqnarray}
0&=&20\log _{10} \frac {K}{\omega T} \\[ 5pt ] 1&=& \frac {K}{\omega T} \\[ 5pt ] \omega &=& \frac {K}{T} \\[ 5pt ] \end{eqnarray}
\] となるので，これらを満たすグラフは(4)と求められる。