《理論》〈電子理論〉[H19:問13]一様磁界中の電子の運動に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

真空中において磁束密度\( \ B \ \mathrm {[T]} \ \)の平等磁界中に，磁界の方向と直角に初速\( \ v \ \mathrm {[m / s]} \ \)で入射した電子は，電磁力\( \ F= \ \fbox {　 （ア） 　} \ \mathrm {[N]} \ \)によって円運動をする。

その円運動の半径を\( \ r \ \mathrm {[m]} \ \)とすれば，遠心力と電磁力とが釣り合うので，円運動の半径は，\( \ r= \ \fbox {　 （イ） 　} \ \mathrm {[m]} \ \)となる。また，円運動の角速度は\( \ \displaystyle \omega =\frac {v}{r} \ \mathrm {[rad / s]} \ \)であるから，円運動の周期は\( \ T= \ \fbox {　 （ウ） 　} \ \mathrm {[s]} \ \)となる。

ただし，電子の質量を\( \ m \ \mathrm {[kg]} \ \)，電荷の大きさを\( \ e \ \mathrm {[C]} \ \)とし，重力の影響は無視できるものとする。

上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる式として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　Bmev　 & 　\displaystyle \frac {mv}{Be}　 & 　\displaystyle \frac {2\pi m}{Be}　 \\
\hline
(2) & 　Bev　 & 　\displaystyle \frac {mv}{Be}　 & 　\displaystyle \frac {2\pi m}{Be}　 \\
\hline
(3) & 　Bmev　 & 　\displaystyle \frac {v}{Be}　 & 　\displaystyle \frac {2\pi m}{Be}　 \\
\hline
(4) & 　Bev　 & 　\displaystyle \frac {mv}{Be}　 & 　\displaystyle \frac {2\pi }{Be}　 \\
\hline
(5) & 　Bmev　 & 　\displaystyle \frac {v}{Be}　 & 　\displaystyle \frac {2\pi }{Be}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

電子の円運動に関する問題です。
電子の円運動はほぼパターン化されている問題なので，一度マスターするとあらゆる出題パターンで対応できます。様々な問題において，ローレンツ力と向心力が等しいという条件から正答を導き出すようにして下さい。

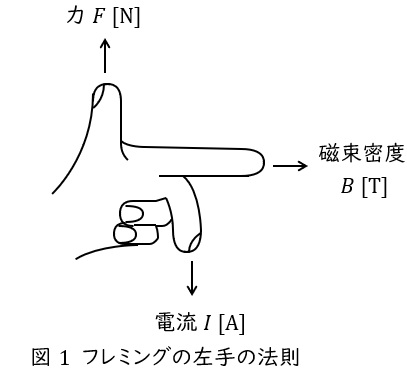
1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電子の速度\( \ v \ \mathrm {[m/s]} \ \)，電子の電荷を\( \ -e \ \mathrm {[C]} \ \)とすると，電子にかかるローレンツ力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&evB \\[ 5pt ] \end{eqnarray}
\] となります。電子の場合，動く向きが電流の向きと逆になるので，中指の向きに注意するようにしましょう。

2.円運動の向心力
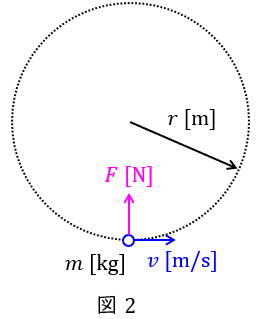
図2のように，質量\( \ m \ \mathrm {[kg]} \ \)の物体が速度\( \ v \ \mathrm {[m / s]} \ \)で半径\( \ r \ \mathrm {[m]} \ \)の円運動をしているとき，物体に加わっている力は円の中心に向かう力（向心力）であり，その大きさ\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&\frac {mv^{2}}{r} \\[ 5pt ] \end{eqnarray}
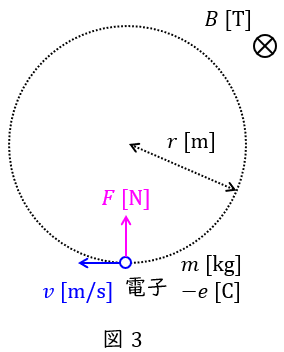
\] となります。電験では電子の円運動の問題で，ローレンツ力が向心力と等しいという条件を使用します。

【解答】

解答：(2)
(ア)
ワンポイント解説「1.フレミングの左手の法則」の通り，磁束密度\( \ B \ \mathrm {[T]} \ \)の平等磁界中に磁界の方向と直角に初速\( \ v \ \mathrm {[m / s]} \ \)で入射した電子に加わる力は\( \ F= Bev \ \mathrm {[N]} \ \)となります。

(イ)
ワンポイント解説「1.フレミングの左手の法則」及び「2.円運動の向心力」の通り，遠心力と電磁力が釣り合うので，
\[
\begin{eqnarray}
\frac {mv^{2}}{r} &=&Bev \\[ 5pt ] \frac {mv}{r} &=&Be \\[ 5pt ] r &=&\frac {mv}{Be} \\[ 5pt ] \end{eqnarray}
\] となります。

(ウ)
円運動の周期\( \ T \ \mathrm {[s]} \ \)は電子が\( \ 1 \ \)周するのに要する時間であるから，
\[
\begin{eqnarray}
T &=&\frac {2\pi r}{v} \\[ 5pt ] &=&\frac {\displaystyle 2\pi \cdot \frac {mv}{Be}}{v} \\[ 5pt ] &=&\frac {2\pi m}{Be} \\[ 5pt ] \end{eqnarray}
\] となります。