《理論》〈電気回路〉[H20:問5]直並列したコンデンサの電荷の動きに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

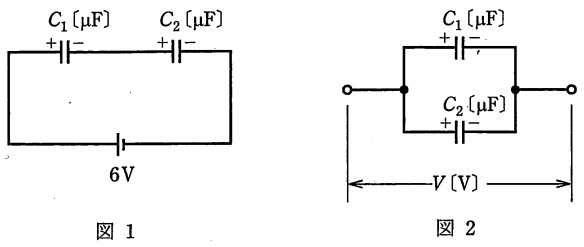
図1に示すように，二つのコンデンサ\( \ C_{1}=4 \ \mathrm {[\mu F]} \ \)と\( \ C_{2}=2 \ \mathrm {[\mu F]} \ \)が直列に接続され，直流電圧\( \ 6 \ \mathrm {[V]} \ \)で充電されている。次に電荷が蓄積されたこの二つのコンデンサを直流電源から切り離し，電荷を保持したまま同じ極性の端子同士を図2に示すように並列に接続する。並列に接続後のコンデンサの端子間電圧の大きさ\( \ V \ \mathrm {[V]} \ \)の値として，正しいのは次のうちどれか。

　(1)　\( \ \displaystyle \frac {2}{3} \ \)　　(2)　\( \ \displaystyle \frac {4}{3} \ \)　　(3)　\( \ \displaystyle \frac {8}{3} \ \)　　(4)　\( \ \displaystyle \frac {16}{3} \ \)　　(5)　\( \ \displaystyle \frac {32}{3} \ \)　　

【ワンポイント解説】

直並列したコンデンサの特性を理解しているかを問う問題です。
合成静電容量を利用しても良いですし，直列接続した場合には蓄えられる電荷量（具体的には図1の\( \ C_{1} \ \)のマイナスの電荷量と\( \ C_{2} \ \)のプラスの電荷量）が等しくなるのでそれを利用して解いても良いかと思います。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.コンデンサの合成静電容量
コンデンサ容量が\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)のコンデンサがある場合，直並列の合成静電容量\( \ C \ \mathrm {[F]} \ \)は下記の通りとなります。抵抗の場合と直並列が逆になることを知っておきましょう。
①並列回路の合成静電容量
\[
\begin{eqnarray}
C&=&C_{1}+C_{2} \\[ 5pt ] \end{eqnarray}
\] ②直列回路の合成静電容量
\[
\begin{eqnarray}
\frac {1}{C}&=&\frac {1}{C_{1}}+\frac {1}{C_{2}} \\[ 5pt ] \end{eqnarray}
\] 整理すると，
\[
\begin{eqnarray}
C&=&\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(3)
図1において，\( \ C_{1}=4 \ \mathrm {[\mu F]} \ \)と\( \ C_{2}=2 \ \mathrm {[\mu F]} \ \)のそれぞれに蓄えられる電荷量は等しいので，その大きさを\( \ Q \ \mathrm {[C]} \ \)とすると，それぞれ分担する電圧\( \ V_{1} \ \mathrm {[V]} \ \)及び\( \ V_{2} \ \mathrm {[V]} \ \)は，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
V_{1}&=&\frac {Q}{C_{1}} \\[ 5pt ] &=&\frac {Q}{4\times 10^{-6}} \\[ 5pt ] V_{2}&=&\frac {Q}{C_{2}} \\[ 5pt ] &=&\frac {Q}{2\times 10^{-6}}=2V_{1}　　・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。\( \ V_{1}+V_{2}=6 \ \mathrm {[V]} \ \)であることから，
\[
\begin{eqnarray}
V_{1}+V_{2}&=&6 \\[ 5pt ] V_{1}+2V_{1}&=&6 \\[ 5pt ] 3V_{1}&=&6 \\[ 5pt ] V_{1}&=&2 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となり，蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)は，
\[
\begin{eqnarray}
Q&=&C_{1}V_{1} \\[ 5pt ] &=&4\times 10^{-6}\times 2 \\[ 5pt ] &=&8\times 10^{-6} \ \mathrm {[C]} \\[ 5pt ] \end{eqnarray}
\] となる。次に，図2のように接続すると，①式より\( \ V_{1}＜V_{2} \ \)であることから\( \ C_{2} \ \)から\( \ C_{1} \ \)に電荷の移動が起こり最終的に二つのコンデンサにかかる電圧は等しくなる。ワンポイント解説「2.コンデンサの合成静電容量」の通り，合成静電容量\( \ C \ \mathrm {[\mu F]} \ \)は，
\[
\begin{eqnarray}
C&=&C_{1}+C_{2} \\[ 5pt ] &=&4\times 10^{-6}+2\times 10^{-6} \\[ 5pt ] &=&6\times 10^{-6} \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}
\] であり，図1及び図2において蓄えられる電荷の総量は\( \ 2Q \ \)で同じであるから，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
2Q&=&CV \\[ 5pt ] \end{eqnarray}
\] の関係が成立するので，これを整理すると，
\[
\begin{eqnarray}
V&=&\frac {2Q}{C} \\[ 5pt ] &=&\frac {2\times 8\times 10^{-6}}{6\times 10^{-6}} \\[ 5pt ] &=&\frac {8}{3} \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。