《理論》〈電磁気〉[H21:問1]平行平板コンデンサの電界、電束密度、電荷に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

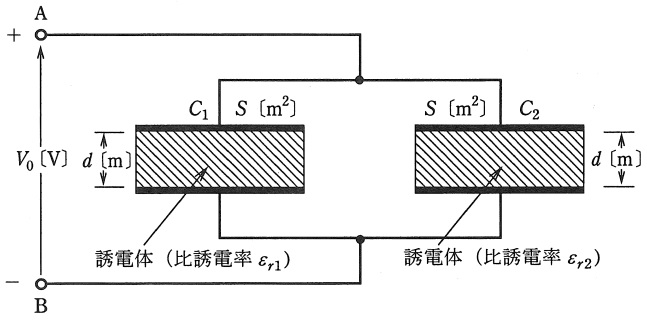
電極板面積と電極板間隔が共に\( \ S \ \mathrm {[m^{2}]} \ \)と\( \ d \ \mathrm {[m]} \ \)で，一方は比誘電率が\( \ \varepsilon _{\mathrm {r1}} \ \)の誘電体からなる平行平板コンデンサ\( \ C_{1} \ \)と，他方は比誘電率が\( \ \varepsilon _{\mathrm {r2}} \ \)の誘電体からなる平行平板コンデンサ\( \ C_{2} \ \)がある。いま，これらを図のように並列に接続し，端子\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)間に直流電圧\( \ V_{0} \ \mathrm {[V]} \ \)を加えた。このとき，コンデンサ\( \ C_{1} \ \)の電極板間の電界の強さを\( \ E_{1} \ \mathrm {[V / m]} \ \)，電束密度を\( \ D_{1} \ \mathrm {[C / m^{2}]} \ \)，また，コンデンサ\( \ C_{2} \ \)の電極板間の電界の強さを\( \ E_{2} \ \mathrm {[V / m]} \ \)，電束密度を\( \ D_{2} \ \mathrm {[C / m^{2}]} \ \)とする。両コンデンサの電界の強さ\( \ E_{1} \ \mathrm {[V / m]} \ \)と\( \ E_{2} \ \mathrm {[V / m]} \ \)はそれぞれ\( \ \fbox {　（ア）　} \ \)であり, 電束密度\( \ D_{1} \ \mathrm {[C / m^{2}]} \ \)と\( \ D_{2} \ \mathrm {[C / m^{2}]} \ \)はそれぞれ\( \ \fbox {　（イ）　} \ \)である。したがって，コンデンサ\( \ C_{1} \ \)に蓄えられる電荷を\( \ Q_{1} \ \mathrm {[C]} \ \)，コンデンサ\( \ C_{2} \ \)に蓄えられる電荷を\( \ Q_{2} \ \mathrm {[C]} \ \)とすると，それらはそれぞれ\( \ \fbox {　（ウ）　} \ \)となる。

ただし，電極板の厚さ及びコンデンサの端効果は，無視できるものとする。また，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とする。

上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる式として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　{\displaystyle E_{1}=\frac {\varepsilon _{\mathrm {r1}}}{d}V_{0}}　\atop 　{\displaystyle E_{2}=\frac {\varepsilon _{\mathrm {r2}}}{d}V_{0}}　 & 　{\displaystyle D_{1}=\frac {\varepsilon _{\mathrm {r1}}}{d}SV_{0}}　\atop 　{\displaystyle D_{2}=\frac {\varepsilon _{\mathrm {r2}}}{d}SV_{0}}　 & 　{\displaystyle Q_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}}　\atop 　{\displaystyle Q_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}}　 \\
\hline
(2) & 　{\displaystyle E_{1}=\frac {\varepsilon _{\mathrm {r1}}}{d}V_{0}}　\atop 　{\displaystyle E_{2}=\frac {\varepsilon _{\mathrm {r2}}}{d}V_{0}}　 & 　{\displaystyle D_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0}}　\atop 　{\displaystyle D_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0}}　 & 　{\displaystyle Q_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}}　\atop 　{\displaystyle Q_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}}　 \\
\hline
(3) & 　{\displaystyle E_{1}=\frac {V_{0}}{d}}　\atop 　{\displaystyle E_{2}=\frac {V_{0}}{d}}　 & 　{\displaystyle D_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}}　\atop 　{\displaystyle D_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}}　 & 　{\displaystyle Q_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0}}　\atop 　{\displaystyle Q_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0}}　 \\
\hline
(4) & 　{\displaystyle E_{1}=\frac {V_{0}}{d}}　\atop 　{\displaystyle E_{2}=\frac {V_{0}}{d}}　 & 　{\displaystyle D_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0}}　\atop 　{\displaystyle D_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0}}　 & 　{\displaystyle Q_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}}　\atop 　{\displaystyle Q_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}}　 \\
\hline
(5) & 　{\displaystyle E_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0}}　\atop 　{\displaystyle E_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0}}　 & 　{\displaystyle D_{1}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0}}　\atop 　{\displaystyle D_{2}=\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0}}　 & 　{\displaystyle Q_{1}=\frac {\varepsilon _{0}}{d}SV_{0}}　\atop 　{\displaystyle Q_{2}=\frac {\varepsilon _{0}}{d}SV_{0}}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

比誘電率の異なる平行平板コンデンサの電界の強さ，電束密度及び蓄えられる電荷の大きさを求める問題です。
平行平板コンデンサの各公式を理解していれば，正答できそうな問題です。平行平板コンデンサはほぼ毎年出題されますので，各公式は必ず覚えておくようにして下さい。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)，極板の面積を\( \ S \ \mathrm {[m^{2}]} \ \)，極板間の距離を\( \ d \ \mathrm {[m]} \ \)とすると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。平行平板コンデンサの間に比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体を挿入すると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

3.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \mathrm {[m]} \ \)の平行平板コンデンサに電圧\( \ V \ \mathrm {[V]} \ \)をかけると，極板間の電界\( \ E \ \mathrm {[V / m]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

4.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係
極板間の誘電率を\( \ \varepsilon \ \)とすると，電束密度\( \ D \ \)と電界\( \ E \ \)には，
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

解答：(4)
(ア)
両コンデンサに加わる電圧が\( \ V_{0} \ \mathrm {[V]} \ \)，電極板間隔が共に\( \ d \ \mathrm {[m]} \ \)であるから，両コンデンサの電界の強さ\( \ E_{1} \ \mathrm {[V / m]} \ \)及び\( \ E_{2} \ \mathrm {[V / m]} \ \)は，ワンポイント解説「3.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
E_{1}&=&\frac {V_{0}}{d} \\[ 5pt ] E_{2}&=&\frac {V_{0}}{d} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(イ)
両コンデンサの電束密度\( \ D_{1} \ \mathrm {[C / m^{2}]} \ \)及び\( \ D_{2} \ \mathrm {[C / m^{2}]} \ \)は，ワンポイント解説「4.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係」の通り，
\[
\begin{eqnarray}
D_{1}&=&\varepsilon _{0}\varepsilon _{\mathrm {r1}}E_{1} \\[ 5pt ] &=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}V_{0} \\[ 5pt ] D_{2}&=&\varepsilon _{0}\varepsilon _{\mathrm {r1}}E_{2} \\[ 5pt ] &=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}V_{0} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(ウ)
両コンデンサの静電容量\( \ C_{1} \ \mathrm {[F]} \ \)及び\( \ C_{2} \ \mathrm {[F]} \ \)は，ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」の通り，
\[
\begin{eqnarray}
C_{1} &=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}} S}{d} \\[ 5pt ] C_{2} &=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}} S}{d} \\[ 5pt ] \end{eqnarray}
\] であるから，各コンデンサに蓄えられる電荷\( \ Q_{1} \ \mathrm {[C]} \ \)及び\( \ Q_{2} \ \mathrm {[C]} \ \)は，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
Q_{1} &=&C_{1}V_{0} \\[ 5pt ] &=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r1}}}{d}SV_{0} \\[ 5pt ] Q_{2} &=&C_{2}V_{0} \\[ 5pt ] &=&\frac {\varepsilon _{0}\varepsilon _{\mathrm {r2}}}{d}SV_{0} \\[ 5pt ] \end{eqnarray}
\] と求められる。