《理論》〈電気回路〉[H21:問10]RL直列回路の過渡現象における抵抗に加わる電圧に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

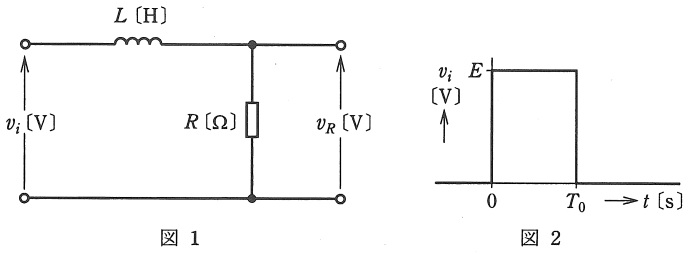
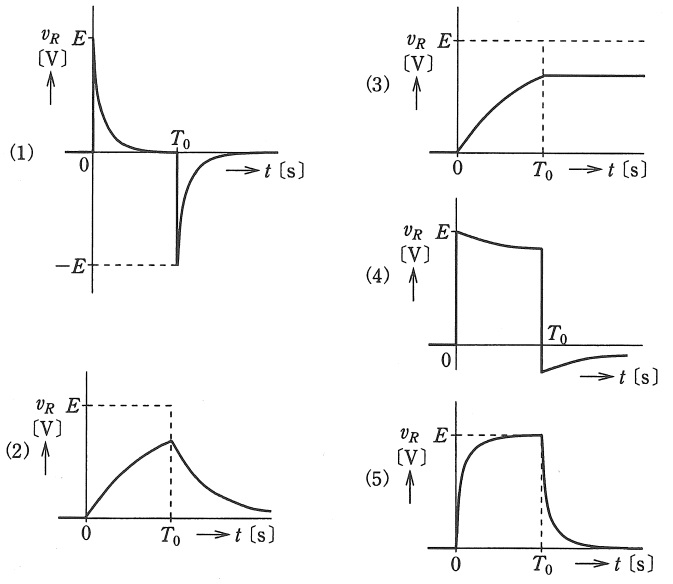
図1のようなインダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルと\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗からなる直列回路に，図2のような振幅\( \ E \ \mathrm {[V]} \ \)，パルス幅\( \ T_{0} \ \mathrm {[s]} \ \)の方形波電圧\( \ v_{i} \ \mathrm {[V]} \ \)を加えた。このときの抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の端子間電圧\( \ v_{R} \ \mathrm {[V]} \ \)の波形を示す図として，正しいのは次のうちどれか。

ただし，図1の回路の時定数\( \ \displaystyle \frac {L}{R} \mathrm {[s]} \ \)は\( \ T_{0} \ \mathrm {[s]} \ \)より十分小さく\( \ ( \displaystyle \frac {L}{R} ≪T_{0}) \ \)，方形波電圧\( \ v_{i} \ \mathrm {[V]} \ \)を発生する電源の内部インピーダンスは\( \ 0 \ \mathrm {[\Omega ]} \ \)とし，コイルに流れる初期電流は\( \ 0 \ \mathrm {[A]} \ \)とする。

【ワンポイント解説】

\( \ RL \ \)直列回路の過渡現象における抵抗\( \ R \ \)の電圧変化を導出する問題です。
抵抗の電圧が電流に比例することを理解した上で，電流の波形を求めれば良いと分かると解きやすくなるかと思います。

1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

2.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので，電流がものすごく流れやすい状態，すなわち短絡として考えます。

② 定常状態
コンデンサに十分に電荷が蓄えられているので，電流をこれ以上蓄えようとしない，すなわち開放として考えます。

【解答】

解答：(5)
\( \ t=0 \ \mathrm {[s]} \ \)において電圧\( \ E \ \mathrm {[V]} \ \)が加わった直後は，リアクトルは開放状態であると考えられるため，回路に電流は流れず\( \ v_{R}=0 \ \mathrm {[V]} \ \)となります。
十分時間が経った定常状態においてはリアクトルは短絡状態であると考えられるため，\( \ v_{R}=v_{i}=E \ \mathrm {[V]} \ \)となり，回路には\( \ \displaystyle \frac {E}{R} \ \mathrm {[A]} \ \)の電流が流れます。

その後\( \ t=T_{0} \ \mathrm {[s]} \ \)において電圧\( \ 0 \ \mathrm {[V]} \ \)になった直後は，リアクトルは電流\( \ \displaystyle \frac {E}{R} \ \mathrm {[A]} \ \)を維持しようとするので，\( \ v_{R}=E \ \mathrm {[V]} \ \)となり，定常状態においてはリアクトルは短絡状態となり，\( \ v_{R}=v_{i}=0 \ \mathrm {[V]} \ \)となります。

以上から，条件を満たす波形は(5)と求められます。