《理論》〈電子理論〉[H22:問11]ホール効果の原理に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，図1及び図2に示す原理図を用いてホール素子の動作原理について述べたものである。

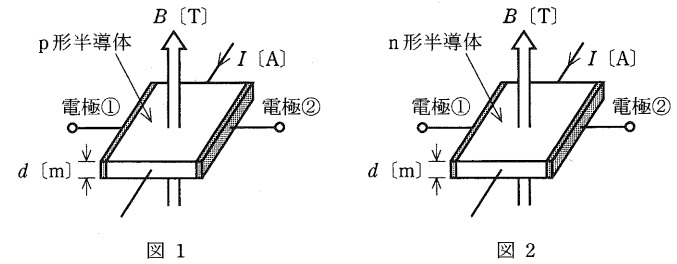
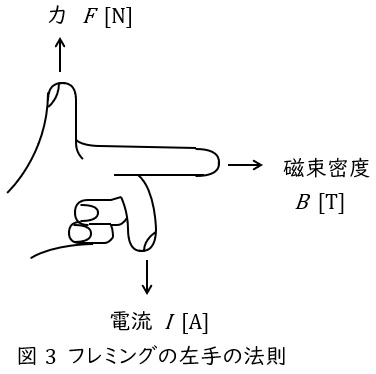
図1に示すように，\( \ \mathrm {p} \ \)形半導体に直流電流\( \ I \ \mathrm {[A]} \ \)を流し，半導体の表面に対して垂直に下から上向きに磁束密度\( \ B \ \mathrm {[T]} \ \)の平等磁界を半導体にかけると，半導体内の正孔は進路を曲げられ，電極①には\( \ \fbox {　（ア）　} \ \)電荷，電極②には\( \ \fbox {　（イ）　} \ \)電荷が分布し，半導体の内部に電界が生じる。また，図2の\( \ \mathrm {n} \ \)形半導体の場合は、電界の方向は\( \ \mathrm {p} \ \)形半導体の方向と\( \ \fbox {　（ウ）　} \ \)である。この電界により，電極①－②間にホール電圧\( \ V_{\mathrm {H}}=R_{\mathrm {H}}\times \ \fbox {　（エ）　} \ \mathrm {[V]} \ \)が発生する。

ただし，\( \ d \ \mathrm {[m]} \ \)は半導体の厚さを示し，\( \ R_{\mathrm {H}} \ \)は比例定数\( \ \mathrm {[m^{3}/C]} \ \)である。

上記の記述中の空白箇所 (ア)，(イ)，(ウ)及び(エ)に当てはまる語句又は式として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　負　 & 　正　 & 　同　じ　 & 　\displaystyle \frac {B}{Id}　 \\
\hline
(2) & 　負　 & 　正　 & 　同　じ　 & 　\displaystyle \frac {Id}{B}　 \\
\hline
(3) & 　正　 & 　負　 & 　同　じ　 & 　\displaystyle \frac {d}{BI}　 \\
\hline
(4) & 　負　 & 　正　 & 　反　対　 & 　\displaystyle \frac {BI}{d}　 \\
\hline
(5) & 　正　 & 　負　 & 　反　対　 & 　\displaystyle \frac {BI}{d}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

ホール効果の原理を問う難問です。
空欄（エ）のホール効果の定量的な導出は，\( \ 2 \ \)種かそれ以上の難易度となります。（ア）～（ウ）がローレンツ力の内容となるので，そこまでを理解し正答できるようになれば一旦は十分と考えて良いでしょう。

1.電界\( \ E \ \mathrm {[V / m]} \ \)により電荷\( \ q \ \mathrm {[C]} \ \)に働く力\( \ F \ \mathrm {[N]} \ \)の大きさ
一様な電界\( \ E \ \mathrm {[V / m]} \ \)が電荷\( \ q \ \mathrm {[C]} \ \)にかかっているとき，この電荷\( \ q \ \)に働く力の大きさ\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] となります。

2.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電流の大きさ\( \ I \ \mathrm {[A]} \ \)，直線状導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，導体に発生する電磁力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
(ア)
ワンポイント解説「2.フレミングの左手の法則」の通り，左手を開いて電流の方向を中指（奥から手前），磁束密度の方向を人差し指（下から上）とすると，親指は電極②→①方向になるため，多数キャリヤである正孔は①側に移動します。
したがって，電極①には正電荷が分布します。

(イ)
（ア）より電極①に正電荷が分布するので，電極②には反対の極性である負電荷が分布します。

(ウ)
フレミングの左手の法則の原理は全く同じですが，\( \ \mathrm {n} \ \)形半導体の場合は電子が多数キャリヤなので，電子が電極①側に移動し，①に負電荷が分布，②に反対の極性である正電荷が分布します。したがって，電界の方向は\( \ \mathrm {p} \ \)形半導体と反対方向となります。

(エ)
正孔の電荷量が\( \ q \ \mathrm {[C]} \ \)，正孔の濃度が\( \ p \ \mathrm {[1 /m^{3}]} \ \)であるとすると，ホール電圧\( \ V_{\mathrm {H}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {H}} &=&\frac {BI}{qpd} \\[ 5pt ] \end{eqnarray}
\] で求められ，\( \ \displaystyle R_{\mathrm {H}}=\frac {1}{qp} \ \)とすれば，
\[
\begin{eqnarray}
V_{\mathrm {H}} &=&R_{\mathrm {H}}\times \frac {BI}{d} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

※導出過程を理解したい場合には電験王ＨＰ1種令和3年理論科目問6を参照して下さい。