Contents
【問題】
【難易度】★☆☆☆☆(易しい)
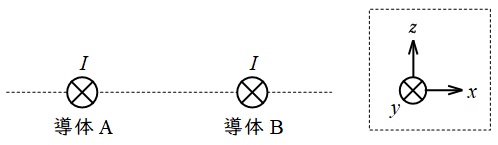
図に示すように,直線導体\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)が\( \ y \ \)方向に平行に配置され,両導体に同じ大きさの電流\( \ I \ \)が共に\( \ +y \ \)方向に流れているとする。このとき,各導体に加わる力の方向について,正しいものを組み合わせたのは次のうちどれか。
なお,\( \ xyz \ \)座標の定義は,破線の枠内の図で示したとおりとする。
\[
\begin{array}{cc}
& 導体 \ \mathrm {A} 導体 \ \mathrm {B} \\
\hline
(1) & +x \ 方向 +x \ 方向 \\
\hline
(2) & +x \ 方向 -x \ 方向 \\
\hline
(3) & -x \ 方向 +x \ 方向 \\
\hline
(4) & -x \ 方向 -x \ 方向 \\
\hline
(5) & どちらの導体にも力は働かない \\
\hline
\end{array}
\]
【ワンポイント解説】
平行導体間に働く力の向きを求める問題です。
本問は向きを求めるだけですが,平成24年問4に力の大きさを求める計算問題も出題されていますので,学習の際には力の大きさも求められるようにしておきましょう。
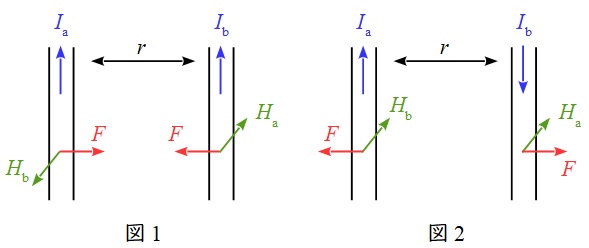
1.平行直線状導体間に働く力の大きさ
図1のような同方向に電流が流れている場合を考えます。電流\( \ I_{\mathrm {b}} \ \)により発生する電流\( \ I_{\mathrm {a}} \ \)が流れる導体部分の磁界の大きさ\( \ H_{\mathrm {b}} \ \)は,アンペールの法則より,
\[
\begin{eqnarray}
H_{\mathrm {b}}&=&\frac {I_{\mathrm {b}}}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となり,空間の透磁率が\( \ \mu \ \)であるとすると,磁束密度\( \ B_{\mathrm {b}} \ \)は,
\[
\begin{eqnarray}
B_{\mathrm {b}}&=&\mu H_{\mathrm {b}} \\[ 5pt ]
&=&\frac {\mu I_{\mathrm {b}}}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となります。フレミングの左手の法則により,\( \ I_{\mathrm {a}} \ \)の流れる導体にかかる力の大きさは引力となり,その\( \ 1 \ \mathrm {[m]} \ \)あたりの大きさ\( \ F \ \mathrm {[N]} \ \)は,
\[
\begin{eqnarray}
F&=&B_{\mathrm {b}} I_{\mathrm {a}}\times 1 \\[ 5pt ]
&=&\frac {\mu I_{\mathrm {a}}I_{\mathrm {b}}}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。同様に\( \ I_{\mathrm {b}} \ \)側や図2のような反対向きの場合も求めることができます。
【解答】
解答:(2)
ワンポイント解説「1.平行直線状導体間に働く力の大きさ」の通り,両導体に同方向の電流を流した場合には共に引き合う力が働くので,導体\( \ \mathrm {A} \ \)には\( \ +x \ \)方向,導体\( \ \mathrm {B} \ \)には\( \ -x \ \)方向の力が働く。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは