《理論》〈電子理論〉[H24:問12]磁界中の電子の運動に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

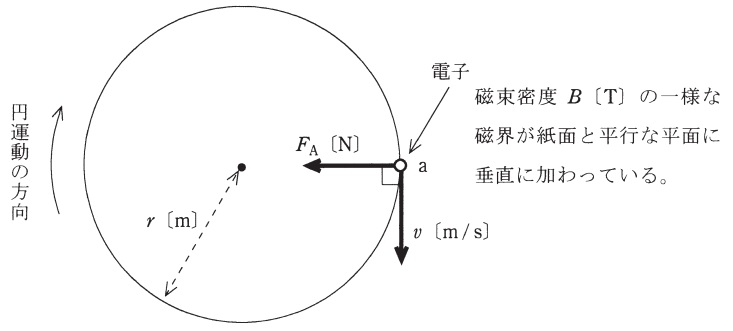
次の文章は，図に示す「磁界中における電子の運動」に関する記述である。

真空中において，磁束密度\( \ B \ \mathrm {[T]} \ \)の一様な磁界が紙面と平行な平面の\( \ \fbox {　 （ア） 　} \ \)へ垂直に加わっている。ここで，平面上の点\( \ \mathrm {a} \ \)に電荷\( \ -e \ \mathrm {[C]} \ \)，質量\( \ m_{0} \ \mathrm {[kg]} \ \)の電子をおき，図に示す向きに速さ\( \ v \ \mathrm {[m／s]} \ \)の初速度を与えると，電子は初速度の向き及び磁界の向きのいずれに対しても垂直で図に示す向きの電磁力\( \ F_{\mathrm {A}} \ \mathrm {[N]} \ \)を受ける。この力のために電子は加速度を受けるが速度の大きさは変わらないので，その方向のみが変化する。したがって，電子はこの平面上で時計回りに速さ\( \ v \ \mathrm {[m／s]} \ \)の円運動をする。この円の半径を\( \ r \ \mathrm {[m]} \ \)とすると，電子の運動は，磁界が電子に作用する電磁力の大きさ\( \ F_{\mathrm {A}}=Bev \ \mathrm {[N]} \ \)と遠心力\( \ \displaystyle F_{\mathrm {B}}=\frac {m_{0}}{r}v^{2} \ \mathrm {[N]} \ \)とが釣り合った円運動であるので，その半径は\( \ r= \ \fbox {　 （イ） 　} \ \mathrm {[m]} \ \)と計算される。したがって，この円運動の周期は\( \ T= \ \fbox {　 （ウ） 　} \ \mathrm {[s]} \ \)，角周波数は\( \ \omega = \ \fbox {　 （エ） 　} \ \mathrm {[rad／s]} \ \)となる。

ただし，電子の速さ\( \ v \ \mathrm {[m／s]} \ \)は，光速より十分小さいものとする。また，重力の影響は無視できるものとする。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 裏からおもて & \displaystyle \frac {m_{0}v}{eB^{2}} & \displaystyle \frac {2\pi m_{0}}{eB} & \displaystyle \frac {eB}{m_{0}} \\
\hline
(2) & おもてから裏 & \displaystyle \frac {m_{0}v}{eB} & \displaystyle \frac {2\pi m_{0}}{eB} & \displaystyle \frac {eB}{m_{0}} \\
\hline
(3) & おもてから裏 & \displaystyle \frac {m_{0}v}{eB} & \displaystyle \frac {2\pi m_{0}}{e^{2}B} & \displaystyle \frac {2e^{2}B}{m_{0}} \\
\hline
(4) & おもてから裏 & \displaystyle \frac {2m_{0}v}{eB} & \displaystyle \frac {2\pi m_{0}}{eB^{2}} & \displaystyle \frac {eB^{2}}{m_{0}} \\
\hline
(5) & 裏からおもて & \displaystyle \frac {m_{0}v}{2eB} & \displaystyle \frac {\pi m_{0}}{eB} & \displaystyle \frac {eB}{m_{0}} \\
\hline
\end{array}
\]

【ワンポイント解説】

磁界中の電子の運動は非常に頻出かつ重要な内容となります。途中の磁界が電子に作用する電磁力の大きさ\( \ F_{\mathrm {A}}=Bev \ \mathrm {[N]} \ \)と遠心力\( \ \displaystyle F_{\mathrm {B}}=\frac {m_{0}}{r}v^{2} \ \mathrm {[N]} \ \)は，どちらも与えられなくても知っている必要があります。

1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \)，電子の速度\( \ v \ \)，電子の電荷を\( \ e \ \)とすると，電子にかかるローレンツ力\( \ F \ \)は
\[
\begin{eqnarray}
F &=&evB \\[ 5pt ] \end{eqnarray}
\] となります。電子の場合，動く向きが電流の向きと逆になるので，中指の向きに注意するようにしましょう。

【解答】

解答：(2)
(ア)
電子の向きが紙面の上から下，ローレンツ力が紙面の右から左なので，フレミングの左手の法則において，中指（電流）は下から上の向き，親指を右から左向きに合わせると人差し指は紙面のおもてから裏側に向く。したがっておもてから裏となる。

(イ)
題意より，
\[
\begin{eqnarray}
F_{\mathrm {A}} &=&F_{\mathrm {B}} \\[ 5pt ] Bev &=&\frac {m_{0}}{r}v^{2} \\[ 5pt ] Be &=&\frac {m_{0}}{r}v \\[ 5pt ] r &=&\frac {m_{0}v}{eB} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(ウ)
周期\( \ T \ \)は，電子が一周回る間にかかる時間なので，
\[
\begin{eqnarray}
T &=&\frac {2\pi r}{v} \\[ 5pt ] &=&\frac {2\pi }{v}\cdot \frac {m_{0}v}{eB} \\[ 5pt ] &=& \frac {2\pi m_{0}}{eB} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(エ)
角周波数\( \ \omega \ \)は\( \ \displaystyle \omega =\frac {v}{r} \ \)の関係があるので，
\[
\begin{eqnarray}
\omega &=&\frac {v}{r} \\[ 5pt ] &=&\frac {v}{\displaystyle \frac {m_{0}v}{eB}} \\[ 5pt ] &=& \frac {eB}{m_{0}} \\[ 5pt ] \end{eqnarray}
\] と求められる。