《理論》〈電気回路〉[H25:問10]RLC直列回路の特性に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

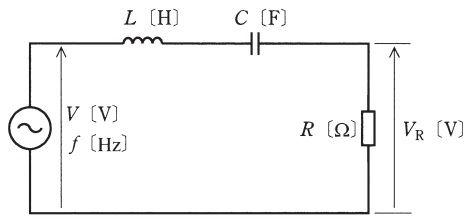
図は，インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルと静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサ，並びに\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗の直列回路に，周波数が\( \ f \ \mathrm {[Hz]} \ \)で実効値が\( \ V(≠0) \ \mathrm {[V]} \ \)である電源電圧を与えた回路を示している。この回路において，抵抗の端子間電圧の実効値\( \ V_{\mathrm {R}} \ \mathrm {[V]} \ \)が零となる周波数\( \ f \ \mathrm {[Hz]} \ \)の条件を全て列挙したものとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{eqnarray}
(1) & \ & 題意を満たす周波数はない \\[ 5pt ] (2) & \ & f=0 \\[ 5pt ] (3) & \ & f=\frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] (4) & \ & f=0，f→∞ \\[ 5pt ] (5) & \ & f=\frac {1}{2\pi \sqrt {LC}}，f→∞ \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

直列の場合，共振周波数はリアクタンス値が零となり，電流が最も流れやすくなる周波数となります。最も電流が流れると抵抗の電圧降下\( \ V_{\mathrm {R}} \ \mathrm {[V]} \ \)がどうなるかを考えてみて下さい。少し引っ掛け問題となっています。

1.コイルやコンデンサのリアクタンス
インダクタンスが\( \ L \ \mathrm {[H]} \ \)のコイル及び静電容量が\( \ C \ \mathrm {[F]} \ \)のコンデンサを周波数\( \ f \ \mathrm {[Hz]} \ \)の交流電源に接続した時のそれぞれのリアクタンスの大きさ\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は，角周波数を\( \ \omega =2\pi f \ \)とすると，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ] &=&\mathrm {j}2\pi f L \\[ 5pt ] -\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] となります。

2.直列回路の共振条件
共振条件は電圧と電流が同位相になる状態で，回路のリアクタンスが零になる状態のことを言います。\(RLC\)直列回路のリアクタンスの共振条件は，角周波数を\( \ \omega =2\pi f \ \)とすると，
\[
\begin{eqnarray}
\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C}&=&0 \\[ 5pt ] \mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) &=& 0 \\[ 5pt ] \omega L &=& \frac {1}{\omega C} \\[ 5pt ] \end{eqnarray}
\] の時共振となり，その共振角周波数と共振周波数は，上式を\( \ \omega \ \)について整理すると，
\[
\begin{eqnarray}
\omega ^{2}&=&\frac {1}{LC} \\[ 5pt ] \omega &=&\frac {1}{\sqrt {LC}} \\[ 5pt ] f &=&\frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【関連する「電気の神髄」記事】

　　直列共振回路の理論

【解答】

解答：(4)
抵抗の端子間電圧の実効値\( \ {\dot V}_{\mathrm {R}} \ \)を電源電圧\( \ \dot V \ \)で表すと，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&\frac {R}{R+\mathrm {j} \omega L +\displaystyle \frac {1}{\mathrm {j} \omega C}} \dot V \\[ 5pt ] &=&\frac {R}{R+\mathrm {j} \left( \omega L -\displaystyle \frac {1}{\omega C}\right) }\dot V \\[ 5pt ] &=&\frac {R}{R+\mathrm {j} \left( 2\pi f L -\displaystyle \frac {1}{2\pi f C}\right) }\dot V \\[ 5pt ] \end{eqnarray}
\] となるので，その大きさ\( \ V_{\mathrm {R}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {R}}&=&\frac {R}{\sqrt {R^{2}+ \left( 2\pi f L -\displaystyle \frac {1}{2\pi f C}\right) ^{2}} }V \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\( \ f=0 \ \)とすると，\( \ 2\pi f L=0 \ \)及び\( \ \displaystyle \frac {1}{2\pi f C}→∞ \ \)となるから，
\[
\begin{eqnarray}
V_{\mathrm {R}}&=&\frac {R}{\sqrt {R^{2}+ \left( 0 -∞\right) ^{2}} }V \\[ 5pt ] &=&0 \\[ 5pt ] \end{eqnarray}
\] となる。また，\( \ f→∞ \ \)とすると，\( \ 2\pi f L→∞ \ \)及び\( \ \displaystyle \frac {1}{2\pi f C}→0 \ \)となるから，
\[
\begin{eqnarray}
V_{\mathrm {R}}&=&\frac {R}{\sqrt {R^{2}+ \left( ∞ -0\right) ^{2}} }V \\[ 5pt ] &=&0 \\[ 5pt ] \end{eqnarray}
\] となる。したがって，正答は(4)となる。