【問題】
【難易度】★★☆☆☆(やや易しい)
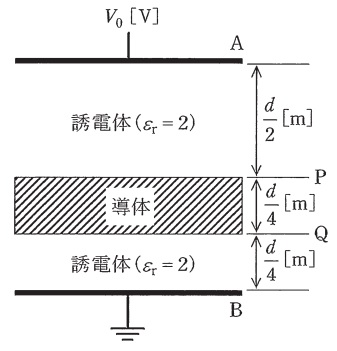
極板\(\mathrm {A-B}\)間が比誘電率\(\varepsilon _{\mathrm {r}}=2\)の誘電体で満たされた平行平板コンデンサがある。極板間の距離は\(d \ \mathrm {[m]}\),極板間の直流電圧は\(V_{0} \ \mathrm {[V]}\)である。極板と同じ形状と大きさをもち,厚さが\(\displaystyle \frac {d}{4} \ \mathrm {[m]}\)の帯電していない導体を図に示す位置\(\mathrm {P-Q}\)間に極板と平行に挿入したとき,導体の電位の値\(\mathrm {[V]}\)として,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,コンデンサの端効果は無視できるものとする。
(1) \(\displaystyle \frac {V_{0}}{8}\) (2) \(\displaystyle \frac {V_{0}}{6}\) (3) \(\displaystyle \frac {V_{0}}{4}\) (4) \(\displaystyle \frac {V_{0}}{3}\) (5) \(\displaystyle \frac {V_{0}}{2}\)
【ワンポイント解説】
毎年のように出題される平行平板コンデンサの問題です。導体中の電位は同じであること,誘電体中の電位の傾き(=電界)は等しいことを理解していれば難なく解けると思います。
1.平行平板コンデンサの静電容量\(C\)の導出
平行平板コンデンサの極板の面積を\(S\),極板間の距離を\(d\),極板間の誘電率を\(\varepsilon \)とすると平行平板コンデンサの静電容量\(C\)は,
\[
C=\frac {\varepsilon S}{d}
\]
となります。
2.平行平板コンデンサの電界\(E\)と電圧\(V\)の関係
極板間の距離\(d\)の平行平板コンデンサに電圧\(V\)をかけると,極板間の電界\(E\)は,
\[
E=\frac {V}{d}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
解答:(4)
誘電体の比誘電率は\(\mathrm {A-P}\)間も\(\mathrm {Q-B}\)間も等しいので,どちらの電界も大きさは等しい。よって,その電界を\(E\)とすると,\(\mathrm {A-P}\)間の電位差\(V_{1}\)と\(\mathrm {Q-B}\)間の電位差\(V_{2}\)は,
\[
\begin{eqnarray}
V_{1} &=&E\cdot \frac {d}{2} \\[ 5pt ]
V_{2} &=&E\cdot \frac {d}{4} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\(V_{1}=2V_{2}\)となる。ここで,\(V_{1}+V_{2}=V_{0}\)であるから,\(\displaystyle V_{1}=\frac {2}{3} V_{0}\),\(\displaystyle V_{2}=\frac {V_{0}}{3} \)と求められ,導体の電位は\(\displaystyle \frac {V_{0}}{3} \)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは