《理論》〈電気回路〉[H26:問6]直流回路の回路計算に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

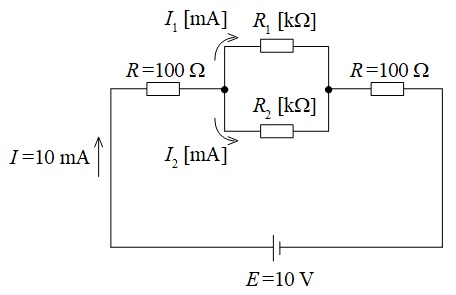
図のように，抵抗を直並列に接続した直流回路がある。この回路に流れる電流\(I\)の値は，\(I=10 \ \mathrm {mA}\)であった。このとき，抵抗\(R_{2} \ \mathrm {[k\Omega ]}\)として，最も近い\(R_{2}\)の値を次の(1)～(5)のうちから一つ選べ。

ただし，抵抗\(R_{1} \ \mathrm {[k\Omega ]}\)に流れる電流\(I_{1} \ \mathrm {[mA]}\)と抵抗\(R_{2} \ \mathrm {[k\Omega ]}\)に流れる電流\(I_{2} \ \mathrm {[mA]}\)の電流比\(\displaystyle \frac {I_{1}}{I_{2}}\)の値は\(\displaystyle \frac {1}{2}\)とする。

(1)　\(0.3\)　　(2)　\(0.6\)　　(3)　\(1.2\)　　(4)　\(2.4\)　　(5)　\(4.8\)

【ワンポイント解説】

キルヒホッフの法則とオームの法則を用いればそれほど難しい問題ではありません。落ち着いて計算するようにして下さい。

【解答】

解答：(3)
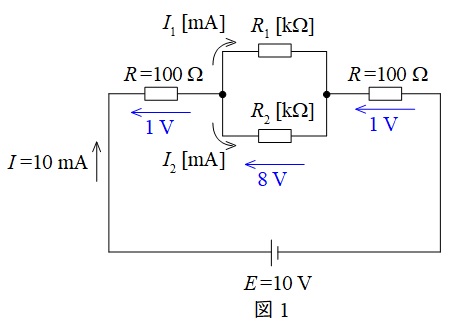
\(R=100 \ \Omega \)の電圧降下\(V_{\mathrm {R}}\)は，
\[
\begin{eqnarray}
V_{\mathrm {R}}&=&RI \\[ 5pt ] &=&100 \times 10\times 10^{-3} \\[ 5pt ] &=&1 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であるので，\(R_{2} \ \mathrm {[k\Omega ]}\)にかかる電圧\(V_{\mathrm {R2}}\)は，
\[
\begin{eqnarray}
V_{\mathrm {R2}}&=&E-V_{\mathrm {R}}-V_{\mathrm {R}} \\[ 5pt ] &=&10-1-1 \\[ 5pt ] &=&8 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。また，題意より\(I_{1} \ \mathrm {[mA]}\)と\(I_{2} \ \mathrm {[mA]}\)の電流比\(\displaystyle \frac {I_{1}}{I_{2}}\)の値は\(\displaystyle \frac {1}{2}\)であるので，
\[
\begin{eqnarray}
I_{2}&=&\frac {2}{3}I \\[ 5pt ] &=&\frac {2}{3}\times 10 \\[ 5pt ] &=&\frac {20}{3} \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，抵抗\(R_{2}\)の大きさは，
\[
\begin{eqnarray}
R_{2}&=&\frac {V_{\mathrm {R2}}}{I_{2}} \\[ 5pt ] &=&\frac {8}{\displaystyle \frac {20}{3}\times 10^{-3}} \\[ 5pt ] &=&1.2\times 10^{3} \ \mathrm {[\Omega ]} →　1.2 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。