《理論》〈電気回路〉[H27:問17]平衡三相交流回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★★（難しい）

図のような\(\mathrm {V}\)結線電源と三相平衡負荷とからなる平衡三相回路において，\(R=5 \ \Omega \)，\(L=16 \ \mathrm {mH}\)である。また，電源の線間電圧\(e_{\mathrm {a}} \ \mathrm {[V]}\)は，時刻\(t \ \mathrm {[s]}\)において，\(e_{\mathrm {a}}=100\sqrt {6}\sin \left( 100\pi t\right) \ \mathrm {[V]}\)と表され，線間電圧\(e_{\mathrm {b}} \ \mathrm {[V]}\)は\(e_{\mathrm {a}} \ \mathrm {[V]}\)に対して振幅が等しく，位相が\(\mathrm {120°}\)遅れている。ただし，電源の内部インピーダンスは零である。このとき，次の(a)及び(b)の問に答えよ。

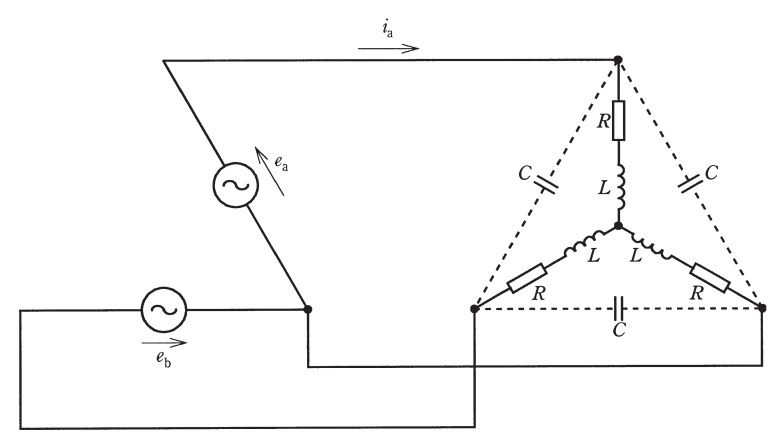
(a)　図の点線で示された配線を切断し，3個のコンデンサを三相回路から切り離したとき，三相電力\(P\)の値\(\mathrm {[kW]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(1\)　　(2)　\(3\)　　(3)　\(6\)　　(4)　\(9\)　　(5)　\(18\)

(b)　点線部を接続することによって同じ特性の3個のコンデンサを接続したところ，\(i_{\mathrm {a}}\)の波形は\(e_{\mathrm {a}}\)の波形に対して位相が\(\mathrm {30°}\)遅れていた。このときのコンデンサ\(C\)の静電容量の値\(\mathrm {[F]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(3.6\times 10^{-5}\)　　(2)　\(1.1\times 10^{-4}\)　　(3)　\(3.2\times 10^{-4}\)
　(4)　\(9.6\times 10^{-4}\)　　(5)　\(2.3\times 10^{-3}\)

【ワンポイント解説】

三相回路の一相等価回路の作成から，\(\Delta -\mathrm {Y}\)変換，さらには複雑な計算もしなければならない難問です。この問題に関してはほぼ二種もしくは一種並みの難易度と言えると思います。

1.リアクトルとコンデンサのリアクタンス
インダクタンスが\(L \ \mathrm {[H]}\)のリアクトルと静電容量\(C \ \mathrm {[F]}\)のコンデンサの各リアクタンス\(X_{\mathrm {L}} \ [\Omega ]\)と\(X_{\mathrm {C}} \ [\Omega ]\)の大きさは，角周波数を\(\omega \ \mathrm {[rad /s]}\)とすると，
\[
\begin{eqnarray}
X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ] X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C } \\[ 5pt ] \end{eqnarray}
\] となります。

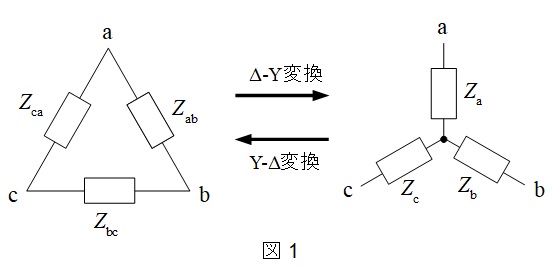
2.\(\Delta -\mathrm {Y}\)変換と\(\mathrm {Y}-\Delta \)変換
①\(\Delta -\mathrm {Y}\)変換
図1において，
\[
\begin{eqnarray}
Z_{\mathrm {a}}&=&\frac {Z_{\mathrm {ab}}Z_{\mathrm {ca}}}{Z_{\mathrm {ab}}+Z_{\mathrm {bc}}+Z_{\mathrm {ca}}} \\[ 5pt ] Z_{\mathrm {b}}&=&\frac {Z_{\mathrm {bc}}Z_{\mathrm {ab}}}{Z_{\mathrm {ab}}+Z_{\mathrm {bc}}+Z_{\mathrm {ca}}} \\[ 5pt ] Z_{\mathrm {c}}&=&\frac {Z_{\mathrm {ca}}Z_{\mathrm {bc}}}{Z_{\mathrm {ab}}+Z_{\mathrm {bc}}+Z_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] ②\(\mathrm {Y}-\Delta \)変換
図1において，
\[
\begin{eqnarray}
Z_{\mathrm {ab}}&=&\frac {Z_{\mathrm {a}}Z_{\mathrm {b}}+Z_{\mathrm {b}}Z_{\mathrm {c}}+Z_{\mathrm {c}}Z_{\mathrm {a}}}{Z_{\mathrm {c}}} \\[ 5pt ] Z_{\mathrm {bc}}&=&\frac {Z_{\mathrm {a}}Z_{\mathrm {b}}+Z_{\mathrm {b}}Z_{\mathrm {c}}+Z_{\mathrm {c}}Z_{\mathrm {a}}}{Z_{\mathrm {a}}} \\[ 5pt ] Z_{\mathrm {ca}}&=&\frac {Z_{\mathrm {a}}Z_{\mathrm {b}}+Z_{\mathrm {b}}Z_{\mathrm {c}}+Z_{\mathrm {c}}Z_{\mathrm {a}}}{Z_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] 平衡三相回路においては，
\[
Z_{\mathrm {ab}}=Z_{\mathrm {bc}}=Z_{\mathrm {ca}}=3Z_{\mathrm {a}}=3Z_{\mathrm {b}}=3Z_{\mathrm {c}}
\] となります。

【関連する「電気の神髄」記事】

　　Y⇔Δ回路のインピーダンス変換式

【解答】

(a)解答：(2)
\(e_{\mathrm {a}}\)の実効値\(E_{\mathrm {a}}\)は，
\[
\begin{eqnarray}
E_{\mathrm {a}}&=&\frac {100\sqrt {6}}{\sqrt {2}} \\[ 5pt ] &=&100\sqrt {3} \ \mathrm {[V]}
\end{eqnarray}
\] であるから，相電圧の実効値\(E_{\mathrm {ap}}\)は，
\[
\begin{eqnarray}
E_{\mathrm {ap}}&=&\frac {100\sqrt {3}}{\sqrt {3}} \\[ 5pt ] &=&100 \ \mathrm {[V]}
\end{eqnarray}
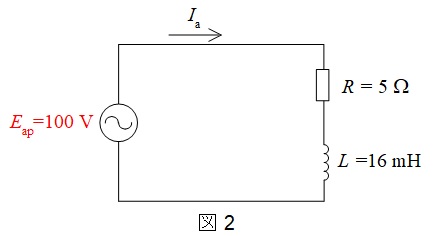
\] となる。負荷は三相平衡であるため，一相分の等価回路を描くと，図2の通りとなる。図2より\(I_{\mathrm {a}}\)は，
\[
\begin{eqnarray}
I_{\mathrm {a}}&=&\frac {E_{\mathrm {ap}}}{\sqrt {R^{2}+(\omega L) ^{2}}} \\[ 5pt ] &=&\frac {100}{\sqrt {5^2+(100 \pi \times 16\times 10^{-3})^{2}}} \\[ 5pt ] &=&14.108 \ \mathrm {[A]}
\end{eqnarray}
\] であるから，三相電力\(P\)は，
\[
\begin{eqnarray}
P&=&3R{I_{\mathrm {a}}}^{2} \\[ 5pt ] &=&3\times 5\times {14.108}^{2} \\[ 5pt ] &≒&2986 \ \mathrm {[W]}　→　3 \ \mathrm {[kW]}
\end{eqnarray}
\] と求められる。

(b)解答：(2)
電源の相電圧\(E_{\mathrm {ap}}\)は，\(E_{\mathrm {a}}\)より30°遅れるので，\(I_{\mathrm {a}}\)は\(E_{\mathrm {ap}}\)と同相になる。すなわち，\(I_{\mathrm {a}}\)を求め，虚数項が零となる静電容量\(C\)が求める値となる。
問題図のコンデンサに対して\(\Delta -\mathrm {Y}\)変換をすると，\(\mathrm {Y}\)回路での静電容量\(C^{\prime }\)は，
\[
\begin{eqnarray}
\frac {1}{\omega C^{\prime }}&=&\frac {1}{3\omega C} \\[ 5pt ] C^{\prime }&=&3C \\[ 5pt ] \end{eqnarray}
\] となるので，一相分の等価回路は図3のようになる。図3において，\(R\)と\(L\)と\(3C\)の合成インピーダンス\(Z\)は，
\[
\begin{eqnarray}
Z&=&\frac {(R+\mathrm {j}\omega L)\frac {1}{\mathrm {j}3\omega C}}{(R+\mathrm {j}\omega L)+\frac {1}{\mathrm {j}3\omega C}} \\[ 5pt ] &=&\frac {R+\mathrm {j}\omega L}{1-3\omega ^{2}LC +\mathrm {j}3\omega RC} \\[ 5pt ] \end{eqnarray}
\] となるので，電流\(I_{\mathrm {a}}\)は，
\[
\begin{eqnarray}
I_{\mathrm {a}}&=&\frac {E_{\mathrm {ap}}}{Z} \\[ 5pt ] &=&E_{\mathrm {ap}}\frac {1-3\omega ^{2}LC +\mathrm {j}3\omega RC}{R+\mathrm {j}\omega L} \\[ 5pt ] &=&E_{\mathrm {ap}}\frac {(1-3\omega ^{2}LC +\mathrm {j}3\omega RC)(R-\mathrm {j}\omega L)}{R^{2}+(\omega L)^{2}} \\[ 5pt ] &=&E_{\mathrm {ap}}\frac {R(1-3\omega ^{2}LC) +3\omega ^{2}RLC+\mathrm {j} [3\omega R^{2}C-\omega L(1-3\omega ^{2}LC)]}{R^{2}+(\omega L)^{2}} \\[ 5pt ] \end{eqnarray}
\] となるので，上式の虚数部が零となればよいから，
\[
\begin{eqnarray}
3\omega R^{2}C-\omega L(1-3\omega ^{2}LC)&=&0 \\[ 5pt ] 3R^{2}C-L(1-3\omega ^{2}LC)&=&0 \\[ 5pt ] 3R^{2}C-L+3\omega ^{2}L^{2}C&=&0 \\[ 5pt ] C&=&\frac {L}{3R^{2}+3\omega ^{2}L^{2}} \\[ 5pt ] \end{eqnarray}
\] となり，各値を代入すると，
\[
\begin{eqnarray}
C&=&\frac {16\times 10^{-3}}{3\times 5 ^{2}+3\times (100 \pi ) ^{2}(16\times 10^{-3})^{2}} \\[ 5pt ] &≒&\frac {16\times 10^{-3}}{75+75.798} \\[ 5pt ] &≒&0.1061\times 10^{-3}　→　1.1 \times 10^{-4} \ \mathrm {[F]}\\[ 5pt ] \end{eqnarray}
\] と求められる。