【問題】
【難易度】★★★☆☆(普通)
次の文章は,平行板コンデンサの電界に関する記述である。
極板間距離\( \ d_{0} \ \mathrm {[m]} \ \)の平行板空気コンデンサの極板間電圧を一定とする。
極板と同形同面積の固体誘電体(比誘電率\(\varepsilon _{\mathrm {r}} > 1\),厚さ\( \ d_{1} \ \mathrm {[m]} < d_{0} \ \mathrm {[m]} \ \))を極板と平行に挿入すると,空気ギャップの電界の強さは,固体誘電体を挿入する前の値と比べて\(\fbox { (ア) }\)。
また,極板と同形同面積の導体(厚さ\( \ d_{2} \ \mathrm {[m]} < d_{0} \ \mathrm {[m]} \ \))を極板と平行に挿入すると,空気ギャップの電界の強さは,導体を挿入する前の値と比べて\(\fbox { (イ) }\)。
ただし,コンデンサの端効果は無視できるものとする。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& (ア) & (イ) \\
\hline
(1) & 強くなる & 強くなる \\
\hline
(2) & 強くなる & 弱くなる \\
\hline
(3) & 弱くなる & 強くなる \\
\hline
(4) & 弱くなる & 弱くなる \\
\hline
(5) & 変わらない & 変わらない \\
\hline
\end{array}
\]
【ワンポイント解説】
解答としては電磁気の公式を用いて定量的に説明していますが,導体を挿入すれば極板間が短くなり反比例する電界の強さは大きくなる,誘電体を挿入すれば空気(≒真空)と導体の中間的な性質を持つ,という感覚を持てば複雑な計算をせずに解けると思います。試験本番では時間削減のためにも定性的な解き方ができると良いと思います。
1.平行平板コンデンサの電界\(E\)と電圧\(V\)の関係
極板間の距離\(d\)の平行平板コンデンサに電圧\(V\)をかけると,極板間の電界\(E\)は,
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.平行平板コンデンサの電束密度\(D\)と電界\(E\)の関係
極板間の誘電率を\(\varepsilon \)とすると,電束密度\(D\)と電界\(E\)には,
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【関連する「電気の神髄」記事】
【解答】
解答:(1)
(ア)
極板間電圧を\(V\),空気の誘電率を\(\varepsilon _{0}\)とすると,誘電体の誘電率は\(\varepsilon _{\mathrm {r}}\varepsilon _{0}\)となる。題意に沿って誘電体挿入前後の図を図1,図2に示す。
図1より,誘電体挿入前の電界の強さ\(E_{1}\)は,
\[
\begin{eqnarray}
E_{1}&=&\frac {V}{d_{0}} \\[ 5pt ]
\end{eqnarray}
\]
となる。
図2において,誘電体挿入後の空気部の電界の強さを\(E_{2}\)とすると,コンデンサ間の電束密度は変わらないので,誘電体部の電界の強さ\(E_{2}^{\prime }\)は,
\[
\begin{eqnarray}
\varepsilon _{\mathrm {r}}\varepsilon _{0}E_{2}^{\prime }&=&\varepsilon _{0}E_{2} \\[ 5pt ]
E_{2}^{\prime }&=&\frac {E_{2}}{\varepsilon _{\mathrm {r}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,極板間の電圧\(V\)は,
\[
\begin{eqnarray}
V&=&E_{2}\left( d_{0}-d_{1}\right) +E_{2}^{\prime }d_{1} \\[ 5pt ]
&=&E_{2}\left( d_{0}-d_{1}\right) +\frac {E_{2}}{\varepsilon _{\mathrm {r}}}d_{1} \\[ 5pt ]
\end{eqnarray}
\]
となるので,上式を\(E_{2}\)について整理すると,
\[
\begin{eqnarray}
E_{2}\left( d_{0}-d_{1}\right) +\frac {E_{2}}{\varepsilon _{\mathrm {r}}}d_{1}&=&V \\[ 5pt ]
E_{2}\left( d_{0}-d_{1}+\frac {1}{\varepsilon _{\mathrm {r}}}d_{1}\right) &=&V \\[ 5pt ]
E_{2} &=&\frac {V}{\displaystyle d_{0}-d_{1}+\frac {1}{\varepsilon _{\mathrm {r}}}d_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となる。\(\varepsilon _{\mathrm {r}} > 1\)なので,右辺の分母は\(d_{0}\)より小さくなるので\(E_{2} > E_{1}\)となる。

(イ)
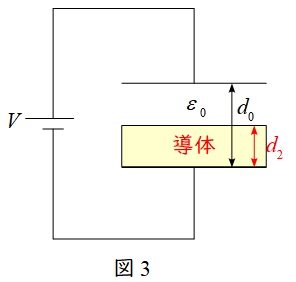
導体を挿入すると,図3のようになる。
図3より,導体を挿入することで極板間の距離が短くなるので,その電界の強さ\(E_{3}\)は,
\[
\begin{eqnarray}
E_{3}&=&\frac {V}{d_{0}-d_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,\(E_{3} > E_{1}\)となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは