《理論》〈電磁気〉[R2:問3]磁界が電流ループに及ぼす電磁力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

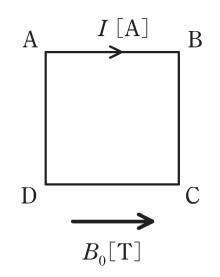
平等な磁束密度\( \ B_{0} \ \mathrm {[T]} \ \)のもとで，一辺の長さが\( \ h \ \mathrm {[m]} \ \)の正方形ループ\( \ \mathrm {ABCD} \ \)に直流電流\( \ I \ \mathrm {[A]} \ \)が流れている。\( \ B_{0} \ \)の向きは辺\( \ \mathrm {AB} \ \)と平行である。\( \ B_{0} \ \)がループに及ぼす電磁力として，正しいものを次の(1)～(5)のうちから一つ選べ。

(1)　大きさ\( \ 2IhB_{0} \ \mathrm {[N]} \ \)の力
(2)　大きさ\( \ 4IhB_{0} \ \mathrm {[N]} \ \)の力
(3)　大きさ\( \ Ih^{2}B_{0} \ \mathrm {[N\cdot m]} \ \)の偶力のモーメント
(4)　大きさ\( \ 2Ih^{2}B_{0} \ \mathrm {[N\cdot m]} \ \)の偶力のモーメント
(5)　力も偶力のモーメントも働かない

【ワンポイント解説】

ループコイルに発生する電磁力に関する問題です。比較的電磁気の問題としては出題されやすいような内容であるかと思います。この問題が理解できたらもう少し難易度が高い平成25年問4の問題も取り組んでみて下さい。

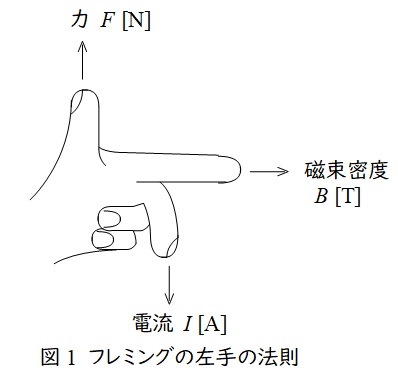
1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電流の大きさ\( \ I \ \mathrm {[A]} \ \)，直線状導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，導体に発生する電磁力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
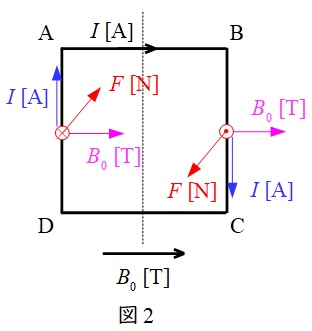
ワンポイント解説「1.フレミングの左手の法則」の通り，磁束密度と電流は角度が直角の時に力が発生するので，電磁力が働くのは辺\( \ \mathrm {BC} \ \)と辺\( \ \mathrm {DA} \ \)に対してとなる。
それぞれの電磁力の向きは図2の通りとなり，力の大きさ\( \ F \ \mathrm {[N]} \ \)はどちらも，
\[
\begin{eqnarray}
F &=&B_{0}Ih \\[ 5pt ] \end{eqnarray}
\] となる。したがって，正方形ループ\( \ \mathrm {ABCD} \ \)は図2の点線を中心に右回りに回転することになり，そのモーメント\( \ M \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
M &=&F\times \frac {h}{2}\times 2 \\[ 5pt ] &=&B_{0}Ih\times \frac {h}{2}\times 2 \\[ 5pt ] &=&Ih^{2}B_{0} \\[ 5pt ] \end{eqnarray}
\] と求められる。