《理論》〈電子理論〉[R3:問13]電界効果トランジスタの簡易小信号等価回路に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

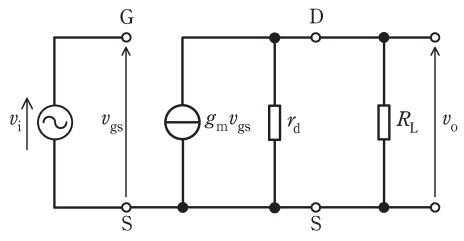
図は，電界効果トランジスタ（\( \ \mathrm {FET} \ \)）を用いたソース接地増幅回路の簡易小信号交流等価回路である。この回路の電圧増幅度\( \ \displaystyle A_{\mathrm {v}}=\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \ \)を近似する式として，正しいものを次の(1)～(5)のうちから一つ選べ。ただし，図中の\( \ \mathrm {S} \ \)，\( \ \mathrm {G} \ \)，\( \ \mathrm {D} \ \)はそれぞれソース，ゲート，ドレインであり，\( \ v_{\mathrm {i}} \ \mathrm {[V]} \ \)，\( \ v_{\mathrm {o}} \ \mathrm {[V]} \ \)，\( \ v_{\mathrm {gs}} \ \mathrm {[V]} \ \)は各部の電圧，\( \ g_{\mathrm {m}} \ \mathrm {[S]} \ \)は\( \ \mathrm {FET} \ \)の相互コンダクタンスである。また，抵抗\( \ r_{\mathrm {d}} \ \mathrm {[\Omega ]} \ \)は抵抗\( \ R_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)に比べて十分大きいものとする。

　(1)　\( \ g_{\mathrm {m}}R_{\mathrm {L}} \ \)　　(2)　\( \ g_{\mathrm {m}}r_{\mathrm {d}} \ \)　　(3)　\( \ g_{\mathrm {m}}\left( R_{\mathrm {L}}+r_{\mathrm {d}}\right) \ \)　　
　(4)　\( \ \displaystyle \frac {g_{\mathrm {m}}r_{\mathrm {d}}}{R_{\mathrm {L}}} \ \)　　(5)　\( \ \displaystyle \frac {g_{\mathrm {m}}R_{\mathrm {L}}}{R_{\mathrm {L}}+r_{\mathrm {d}}} \ \)

【ワンポイント解説】

小信号等価回路を用いた計算問題です。
小信号等価回路は基本的に回路が与えられているので，実質回路計算の問題となります。
慣れてしまえば確実に得点できる問題なので，確実に理解しておくようにしましょう。

【解答】

解答：(1)
問題図より入力側に関して，
\[
\begin{eqnarray}
v_{\mathrm {i}}&=&v_{\mathrm {gs}} \\[ 5pt ] \end{eqnarray}
\] である。一方出力側に関して，\( \ r_{\mathrm {d}} \ \mathrm {[\Omega ]} \ \)は\( \ R_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)に比べて十分に大きいので，電流源\( \ g_{\mathrm {m}}v_{\mathrm {gs}} \ \)の電流は\( \ r_{\mathrm {d}} \ \mathrm {[\Omega ]} \ \)には流れず，全て\( \ R_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)に流れると考えられるので，
\[
\begin{eqnarray}
v_{\mathrm {o}}&=&-R_{\mathrm {L}}\cdot g_{\mathrm {m}}v_{\mathrm {gs}} \\[ 5pt ] &=&-g_{\mathrm {m}}R_{\mathrm {L}}v_{\mathrm {gs}} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，この回路の電圧増幅度\( \ \displaystyle A_{\mathrm {v}}=\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \ \)は，
\[
\begin{eqnarray}
A_{\mathrm {v}}&=&\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \\[ 5pt ] &=&\left| \frac {-g_{\mathrm {m}}R_{\mathrm {L}}v_{\mathrm {gs}}}{v_{\mathrm {gs}}}\right| \\[ 5pt ] &=&\left| -g_{\mathrm {m}}R_{\mathrm {L}}\right| \\[ 5pt ] &=&g_{\mathrm {m}}R_{\mathrm {L}} \\[ 5pt ] \end{eqnarray}
\] と求められる。