《理論》〈電気及び電子計測〉[R3:問16]電流計及び負荷の消費電力の誤差率に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

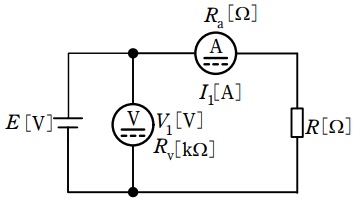
図のように，電源\( \ E \ \mathrm {[V]} \ \)，負荷抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，内部抵抗\( \ R_{\mathrm {v}} \ \mathrm {[k\Omega ]} \ \)の電圧計及び内部抵抗\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)の電流計を接続した回路がある。この回路において，電圧計及び電流計の指示値がそれぞれ\( \ V_{\mathrm {1}} \ \mathrm {[V]} \ \)，\( \ I_{\mathrm {1}} \ \mathrm {[A]} \ \)であるとき，次の(a)及び(b)の問に答えよ。ただし，電圧計と電流計の指示値の積を負荷抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の消費電力の測定値とする。

(a)　電流計の電力損失の値\( \ \mathrm {[W]} \ \)を表す式として，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ \displaystyle \frac {V_{1}^{2}}{R_{\mathrm {a}}} \ \)　　(2)　\( \ \displaystyle \frac {V_{1}^{2}}{R_{\mathrm {a}}}-I_{1}^{2}R_{\mathrm {a}} \ \)　　(3)　\( \ \displaystyle \frac {V_{1}^{2}}{R_{\mathrm {v}}}+I_{1}^{2}R_{\mathrm {a}} \ \)　
　(4)　\( \ I_{1}^{2}R_{\mathrm {a}} \ \)　　(5)　\( \ I_{1}^{2}R_{\mathrm {a}}-I_{1}^{2}R_{\mathrm {v}} \ \)

(b)　今，負荷抵抗\( \ R=320 \ \mathrm {\Omega } \ \)，電流計の内部抵抗\( \ R_{\mathrm {a}}=4 \ \mathrm {\Omega } \ \)が分かっている。
　この回路で得られた負荷抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の消費電力の測定値\( \ V_{\mathrm {1}}I_{\mathrm {1}} \ \mathrm {[W]} \ \)に対して，\( \ R \ \mathrm {[\Omega ]} \ \)の消費電力を真値とするとき，誤差率の値\( \ \mathrm {[％]} \ \)として最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.3 \ \)　　(2)　\( \ 0.8 \ \)　　(3)　\( \ 0.9 \ \)　　(4)　　\( \ 1.0 \ \)　　(5)　\( \ 1.2 \ \)

【ワンポイント解説】

電気測定における電圧計と電流計の誤差率に関する問題です。
(a)は非常に易しい問題，(b)は少しコツが必要な問題ですがそれほど難解なものではありません。
誤差率を定義をしっかりと理解するようにしましょう。

1.誤差及び誤差率の定義
真値を\( \ T \ \)，測定値を\( \ M \ \)とすると，誤差\( \ \varepsilon \ \)と誤差率\( \ ％\varepsilon \ \)は，
\[
\begin{eqnarray}
\varepsilon &=&M-T \\[ 5pt ] ％\varepsilon &=&\frac {M-T}{T} \times 100 \ [％] \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(4)
電流計の電力損失\( \ P_{\mathrm {a}} \ \mathrm {[W]} \ \)は，内部抵抗\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)，電流計を流れる電流が\( \ I_{\mathrm {1}} \ \mathrm {[A]} \ \)であるから，
\[
\begin{eqnarray}
P_{\mathrm {a}} &=&I_{\mathrm {1}}^{2}R_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(5)
電圧計の測定値\( \ V_{\mathrm {1}} \ \mathrm {[V]} \ \)は，\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)と\( \ R \ \mathrm {[\Omega ]} \ \)の電圧降下に等しいので，
\[
\begin{eqnarray}
V_{\mathrm {1}} &=&\left( R_{\mathrm {a}}+R\right) I_{\mathrm {1}} \\[ 5pt ] &=&\left( 4+320\right) I_{\mathrm {1}} \\[ 5pt ] &=&324 I_{\mathrm {1}} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「1.誤差及び誤差率の定義」より，誤差率\( \ ％\varepsilon \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％\varepsilon &=&\frac {V_{\mathrm {1}}I_{\mathrm {1}}-RI_{\mathrm {1}}^{2}}{RI_{\mathrm {1}}^{2}} \times 100 \\[ 5pt ] &=&\frac {324I_{\mathrm {1}}^{2}-320I_{\mathrm {1}}^{2}}{320I_{\mathrm {1}}^{2}} \times 100 \\[ 5pt ] &=&\frac {324-320}{320} \times 100 \\[ 5pt ] &=&1.25 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。