Contents
【問題】
【難易度】★★★★★(難しい)
図1の回路は,電流帰還バイアス回路に結合容量を介して,微小な振幅の交流電圧を加えている。この入力電圧の振幅が\( \ A_{\mathrm {i}}=100 \ \mathrm {mV} \ \),角周波数が\( \ \omega =10 \ 000 \ \mathrm {rad/s} \ \)で,時刻\( \ t \ \mathrm {[s]} \ \)に対して\( \ v_{\mathrm {i}}\left( t \right) \ \mathrm {[mV]} \ \)が\( \ v_{\mathrm {i}}\left( t \right) =A_{\mathrm {i}} \sin \omega t \ \)と表されるとき,次の(a)及び(b)の問に答えよ。
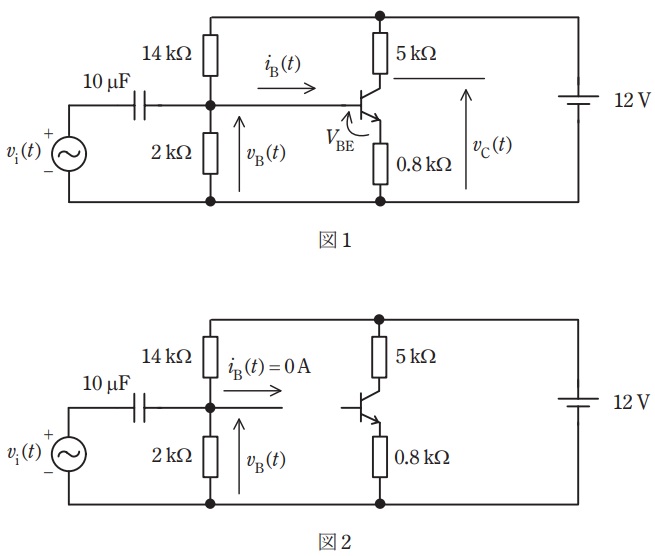
(a) 次の文章は,電圧\( \ v_{\mathrm {B}}\left( t \right) \ \)に関する記述である。
トランジスタのベース端子に流れ込む電流\( \ i_{\mathrm {B}}\left( t \right) \ \)が十分に小さいとき,ベース端子を切り離しても\( \ 2 \ \mathrm {k\Omega } \ \)の抵抗の電圧は変化しない。そこで,図2の回路で考え,さらに重ね合わせの理を用いることで,電圧\( \ v_{\mathrm {B}}\left( t \right) \ \)を求める。まず,\( \ v_{\mathrm {i}}\left( t \right) =0 \ \mathrm {V} \ \)とすることで,直流電圧\( \ V_{\mathrm {B}}= \ \fbox { (ア) } \ \mathrm {V} \ \)が求められる。次に,直流電圧源の値を\( \ 0 \ \mathrm {V} \ \)とし,コンデンサのインピーダンスが\( \ 2 \ \mathrm {k\Omega } \ \)より十分に小さいと考えると,交流電圧\( \ v_{\mathrm {B}}\left( t \right) \ \)の振幅\( \ A_{\mathrm {B}}= \ \fbox { (イ) } \ \mathrm {mV} \ \)と初期位相\( \ \theta _{\mathrm {B}}= \ \fbox { (ウ) } \ \mathrm {rad} \ \)が求められる。以上より,\( \ v_{\mathrm {B}}\left( t \right) =V_{\mathrm {B}}+A_{\mathrm {B}}\sin \left( \omega t +\theta _{\mathrm {B}}\right) \ \)と表すことができる。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして,最も近いものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& (ア) & (イ) & (ウ) \\
\hline
(1) & 0.8 & 71 & 0 \\
\hline
(2) & 0.8 & 100 & \displaystyle \frac {\pi }{4} \\
\hline
(3) & 1.5 & 71 & \displaystyle \frac {\pi }{4} \\
\hline
(4) & 1.5 & 100 & 0 \\
\hline
(5) & 1.5 & 71 & 0 \\
\hline
\end{array}
\]
(b) 図1の回路の電圧\( \ v_{\mathrm {C}}\left( t \right) \ \)を求め,適当な定数\( \ V_{\mathrm {C}} \ \),\( \ A_{\mathrm {C}} \ \),\( \ \theta _{\mathrm {C}} \ \)を用いて\( \ v_{\mathrm {C}}\left( t \right) =V_{\mathrm {C}}+A_{\mathrm {C}}\sin \left( \omega t+\theta _{\mathrm {C}} \right)\ \)と表す。\( \ V_{\mathrm {C}} \ \),\( \ A_{\mathrm {C}} \ \),\( \ \theta _{\mathrm {C}} \ \)に最も近い値の組合せを次の(1)~(5)のうちから一つ選べ。
ただし,ベース・エミッタ間電圧は常に\( \ 0.7 \ \mathrm {V} \ \)であると近似して考えてよい。
\[
\begin{array}{cccc}
& V_{\mathrm {C}} \ \mathrm {[V]} & A_{\mathrm {C}} \ \mathrm {[V]} & \theta _{\mathrm {C}} \ \mathrm {[rad]} \\
\hline
(1) & 5 & 0.6 & 0 \\
\hline
(2) & 5 & 6 & 0 \\
\hline
(3) & 5 & 6 & \pi \\
\hline
(4) & 7 & 0.6 & \pi \\
\hline
(5) & 7 & 6 & \pi \\
\hline
\end{array}
\]
【ワンポイント解説】
電流帰還バイアス回路に関する問題です。
(a)は比較的取り組みやすいかもしれませんが,(b)が難易度が高い問題かと思います。
ただし,電流帰還バイアス回路は解法のパターンがありますので,慣れてしまえば本問も十分に解ける問題です。
本問でコツを掴んで当日出題された際に選択できるようになると理想かと思います。
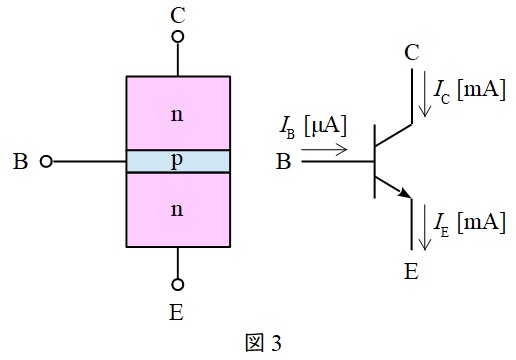
1.バイポーラトランジスタの特徴
\( \ \mathrm {n} \ \)形半導体と\( \ \mathrm {p} \ \)形半導体を\( \ \mathrm {npn} \ \)もしくは\( \ \mathrm {pnp} \ \)にサンドイッチした構造の素子で,電験では\( \ \mathrm {npn} \ \)形が出題されます。
図3のように,各端子はベース\( \ \left( \mathrm {B}\right) \ \),コレクタ\( \ \left( \mathrm {C}\right) \ \),エミッタ\( \ \left( \mathrm {E}\right) \ \)と呼ばれ,ベース\( \ \left( \mathrm {B}\right) \ \)に小さな電流\( \ I_{\mathrm {B}} \ \)を流すと素子がオンとなり,コレクターエミッタ間に比較的大きなコレクタ電流\( \ I_{\mathrm {C}} \ \)が流れます。
エミッタ電流\( \ I_{\mathrm {E}} \ \)は\( \ I_{\mathrm {B}}+I_{\mathrm {C}} \ \)となりますが,ベース電流\( \ I_{\mathrm {B}} \ \)は十分に小さく\( \ I_{\mathrm {E}}≒I_{\mathrm {C}} \ \)とすることも多いです。
ベース電流\( \ I_{\mathrm {B}} \ \)の電流を止めると素子がオフとなり,コレクタ電流\( \ I_{\mathrm {C}} \ \)も流れなくなります。
【解答】
(a)解答:(4)
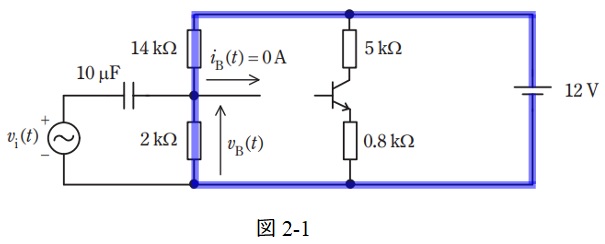
(ア)
図2-1に示す閉回路に分圧の法則を適用すると,
\[
\begin{eqnarray}
V_{\mathrm {B}}&=&\frac {2\times 10^{3}}{2\times 10^{3}+14\times 10^{3}}\times 12 \\[ 5pt ]
&=&1.5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
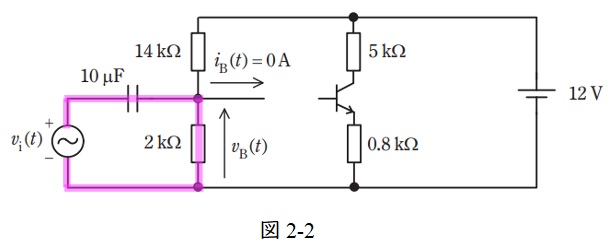
(イ)
図2-2に示す回路について,コンデンサのインピーダンスが十分に小さく電圧降下がないと考えると,交流電圧\( \ v_{\mathrm {B}}\left( t \right) \ \)の振幅\( \ v_{\mathrm {i}}\left( t \right) \ \)と同じ大きさの振幅\( \ A_{\mathrm {B}}= 100 \ \mathrm {[mV]} \ \)が現れることになる。
(ウ)
(イ)と同様に,コンデンサのインピーダンスが十分に小さいとすると,\( \ v_{\mathrm {B}}\left( t \right) \ \)は\( \ v_{\mathrm {i}}\left( t \right) \ \)と等しくなるので,位相差はなく\( \ \theta _{\mathrm {B}}=0 \ \mathrm {rad} \ \)と求められる。
(b)解答:(4)
(a)より,\( \ v_{\mathrm {B}}\left( t \right) =1.5+0.1\sin \omega t \ \mathrm {[V]} \ \)であり,ベース・エミッタ間電圧は\( \ 0.7 \ \mathrm {V} \ \)であるから,エミッタ電圧\( \ v_{\mathrm {E}}\left( t \right) \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {E}}\left( t \right) &=&v_{\mathrm {B}}\left( t \right) -0.7 \\[ 5pt ]
&=&1.5+0.1\sin \omega t -0.7 \\[ 5pt ]
&=&0.8+0.1\sin \omega t \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,エミッタ電流\( \ i_{\mathrm {E}}\left( t \right) \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
i_{\mathrm {E}}\left( t \right) &=&\frac {v_{\mathrm {E}}\left( t \right) }{0.8\times 10^{3}} \\[ 5pt ]
&=&\frac {0.8+0.1\sin \omega t}{0.8\times 10^{3}} \\[ 5pt ]
&=&\left( 1.0+0.125\sin \omega t \right) \times 10^{-3} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,ベース電流は十分に小さいとすれば,コレクタ電流は\( \ i_{\mathrm {C}}\left( t \right) \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
i_{\mathrm {C}}\left( t \right) &≒&i_{\mathrm {E}}\left( t \right) \\[ 5pt ]
&=&\left( 1.0+0.125\sin \omega t \right) \times 10^{-3} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,コレクタ電圧\( \ v_{\mathrm {C}}\left( t \right) \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {C}}\left( t \right) &=&12-5\times 10^{3}\times i_{\mathrm {C}}\left( t \right) \\[ 5pt ]
&=&12-5\times 10^{3}\times \left( 1.0+0.125\sin \omega t \right) \times 10^{-3} \\[ 5pt ]
&=&12- 5-0.625\sin \omega t \\[ 5pt ]
&=&7-0.625\sin \omega t \\[ 5pt ]
&=&7+0.625\sin \left( \omega t+\pi \right) \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは