《理論》〈電子理論〉[R05下:問13]縦続接続した増幅器の電圧利得の導出に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

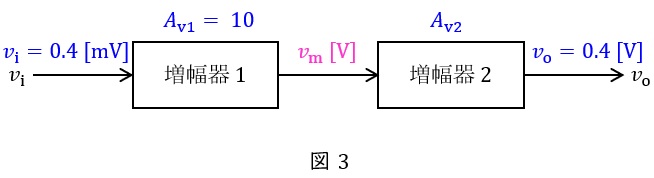
図に示すように二つの増幅器を縦続接続した回路があり，増幅器\( \ 1 \ \)の電圧増幅度は\( \ 10 \ \)である。今，入力電圧\( \ v_{\mathrm {i}} \ \)の値として\( \ 0.4 \ \mathrm {mV} \ \)の信号を加えたとき，出力電圧\( \ v_{\mathrm {o}} \ \)の値は\( \ 0.4 \ \mathrm {V} \ \)であった。増幅器\( \ 2 \ \)の電圧利得の値\( \ \mathrm {[dB]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 10 \ \)　　(2)　\( \ 20 \ \)　　(3)　\( \ 40 \ \)　　(4)　\( \ 50 \ \)　　(5)　\( \ 60 \ \)　　

【ワンポイント解説】

縦続接続した増幅器の電圧利得の導出に関する問題です。
内容自体は機械科目の自動制御の分野で扱う内容ですので，理論科目のテキストには掲載されていない場合もあるかと思います。
電圧利得の式が与えられていないこと及び科目を超えた内容ということで少し受験生によっては厳しいと感じたかもしれません。
本問は平成12年問7からの再出題となります。

1.ブロック線図の考え方（機械科目）
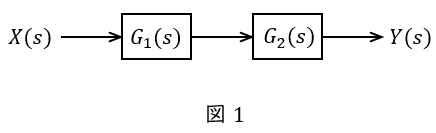
①直列
図1のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ] \end{eqnarray}
\] となります。

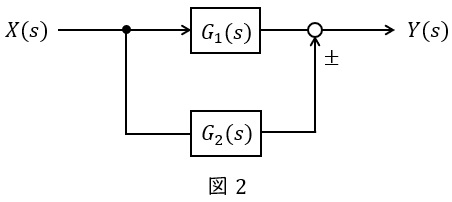
②並列
図2のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ] \end{eqnarray}
\] となります。

2.ゲイン\( \ g \ \)（電圧利得）
電圧増幅率が\( \ \displaystyle A_{\mathrm {v}} =\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \ \)で与えられる時，ゲイン\( \ g \ \mathrm {[dB]} \ \)は，
\[
\begin{eqnarray}
g&=&20\log _{10} A_{\mathrm {v}} \\[ 5pt ] &=&20\log _{10} \left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(3)
図3に示すように，増幅器\( \ 1 \ \)と増幅器\( \ 2 \ \)の間の電圧を\( \ v_{\mathrm {m}} \ \mathrm {[V]} \ \)とすると，増幅器\( \ 1 \ \)の電圧増幅度\( \ A_{\mathrm {v1}}=10 \ \)なので，
\[
\begin{eqnarray}
v_{\mathrm {m}}&=&A_{\mathrm {v1}} v_{\mathrm {i}} \\[ 5pt ] &=&10\times 0.4\times 10^{-3} \\[ 5pt ] &=&0.004 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。また，出力電圧\( \ v_{\mathrm {o}}=0.4 \ \mathrm {[V]} \ \)であるから，増幅器\( \ 2 \ \)の電圧増幅度\( \ A_{\mathrm {v2}} \ \)は，
\[
\begin{eqnarray}
A_{\mathrm {v2}}&=&\frac {v_{\mathrm {o}}}{v_{\mathrm {m}}} \\[ 5pt ] &=&\frac {0.4}{0.004} \\[ 5pt ] &=&100 \\[ 5pt ] \end{eqnarray}
\] となる。よって，増幅器\( \ 2 \ \)の電圧利得\( \ g_{2} \ \mathrm {[dB]} \ \)は，ワンポイント解説「2.ゲイン\( \ g \ \)（電圧利得）」の通り，
\[
\begin{eqnarray}
g_{2}&=&20\log _{10} A_{\mathrm {v2}} \\[ 5pt ] &=&20\log _{10} 100 \\[ 5pt ] &=&20\times 2 \\[ 5pt ] &=&40 \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] と求められる。