《理論》〈電磁気〉[R06下:問3]コイルの鎖交磁束が変化したときに発生する起電力に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

巻数\( \ 30 \ \)のコイルを貫通している磁束が\( \ 0.1 \ \)秒間に\( \ 1 \ \mathrm {Wb} \ \)の割合で直線的に変化するとき，コイルに発生する起電力の大きさ\( \ \mathrm {[V]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 250 \ \)　　(2)　\( \ 300 \ \)　　(3)　\( \ 350 \ \)　　(4)　\( \ 400 \ \)　　(5)　\( \ 450 \ \)

【ワンポイント解説】

ファラデーの電磁誘導の法則の公式に各値を代入して解く問題です。
本問は公式に代入して計算するだけの問題なので，電験としてはかなり解きやすい問題となります。ほとんどの合格者は正答してくると思われますので，本問のような問題は確実に得点できるように準備しましょう。
本問はやや古いですが平成9年問2からの再出題となります。

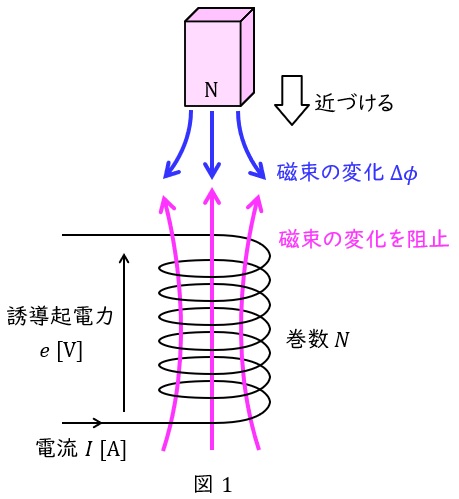
1.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)
図1に示すように，巻数\( \ N \ \)のコイルを貫通する磁束\( \ \phi \ \mathrm {[Wb]} \ \)があるとき，ファラデーの電磁誘導の法則より，コイルに発生する誘導起電力\( \ e \ \mathrm {[V]} \ \)は，磁束の時間変化\( \ \displaystyle \frac {\Delta \phi }{\Delta t} \ \)に比例し，
\[
\begin{eqnarray}
e&=&−N\frac {\Delta \phi }{\Delta t} \\[ 5pt ] \end{eqnarray}
\] で求められます。これをファラデーの電磁誘導の法則といいます。一方，電流変化\( \ \Delta I \ \mathrm {[A]} \ \)を考える場合，
\[
\begin{eqnarray}
e&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] \end{eqnarray}
\] という関係も成り立ち，\( \ L \ \mathrm {[H]}\ \)を自己インダクタンスと言います。これらの関係から，
\[
\begin{eqnarray}
−N\frac {\Delta \phi }{\Delta t}&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

解答：(2)
巻数\( \ N=30 \ \)のコイルを貫通している磁束が\( \ \Delta t=0.1 \ \mathrm {[s]} \ \)の間に\( \ \Delta \phi =1 \ \mathrm {[Wb]} \ \)変化しているので，コイルに発生する起電力の大きさ\( \ e \ \mathrm {[V]} \ \)は，ワンポイント解説「1.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)」の通り，
\[
\begin{eqnarray}
e&=&−N\frac {\Delta \phi }{\Delta t} \\[ 5pt ] &=&−30\times \frac {1}{0.1} \\[ 5pt ] &=&−300 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，大きさは\( \ 300 \ \mathrm {V} \ \)と求められる。