《理論》〈電気回路〉[R06下:問9]周波数が変化したときにRC回路に流れる電流に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

\( \ 4 \ \mathrm {\Omega } \ \)の抵抗と静電容量が\( \ C \ \mathrm {[F]} \ \)のコンデンサを直列に接続した\( \ RC \ \)回路がある。この\( \ RC \ \)回路に，周波数\( \ 50 \ \mathrm {Hz} \ \)の交流電圧\( \ 100 \ \mathrm {V} \ \)の電源を接続したところ，\( \ 20 \ \mathrm {A} \ \)の電流が流れた。では，この\( \ RC \ \)回路に，周波数\( \ 60 \ \mathrm {Hz} \ \)の交流電圧\( \ 100 \ \mathrm {V} \ \)の電源を接続したとき，\( \ RC \ \)回路に流れる電流の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 16.7 \ \)　　(2)　\( \ 18.6 \ \)　　(3)　\( \ 21.2 \ \)　　(4)　\( \ 24.0 \ \)　　(5)　\( \ 25.6 \ \)

【ワンポイント解説】

周波数の異なる電源に切り替えたときの回路に流れる電流の変化を考える問題です。
一気に求めようとすると間違いが発生しやすくなるので，一つ一つ丁寧に解いていくと良いかと思います。
本問は平成25年問7からの再出題となります。

1.抵抗，コイル，コンデンサのインピーダンスとアドミタンス
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンス\( \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，アドミタンス\( \ \mathrm {[S]} \ \)はインピーダンスの逆数なので，
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {R}}&=&\frac {1}{R}&& \\[ 5pt ] {\dot Y}_{\mathrm {L}}&=&\frac {1}{\mathrm {j}\omega L}&=&\frac {1}{\mathrm {j}2\pi f L} \\[ 5pt ] {\dot Y}_{\mathrm {C}}&=&\mathrm {j}\omega C&=&\mathrm {j}2\pi f C \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(3)
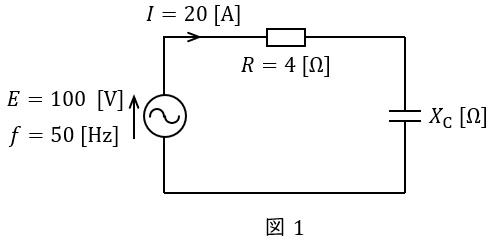
周波数\( \ 50 \ \mathrm {Hz} \ \)の交流電源に接続したときの回路図を図1に示す。
回路全体のインピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
Z&=&\frac {E}{I} \\[ 5pt ] &=&\frac {100}{20} \\[ 5pt ] &=&5 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，コンデンサのリアクタンス\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
X_{\mathrm {C}}&=&\sqrt {Z^{2}-R^{2}} \\[ 5pt ] &=&\sqrt {5^{2}-4^{2}} \\[ 5pt ] &=&3 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。

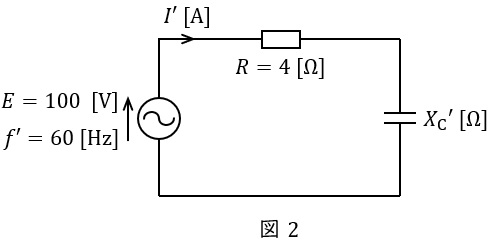
次に，周波数\( \ 60 \ \mathrm {Hz} \ \)の交流電源に接続したときの回路図を図2に示す。
ワンポイント解説「1.抵抗，コイル，コンデンサのインピーダンスとアドミタンス」の通り，コンデンサのリアクタンスは周波数に反比例するので，\( \ f^{\prime }= 60 \ \mathrm {[Hz]} \ \)のときのコンデンサのリアクタンス\( \ {X_{\mathrm {C}}}^{\prime } \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
{X_{\mathrm {C}}}^{\prime }&=&\frac {f}{f^{\prime }}X_{\mathrm {C}} \\[ 5pt ] &=&\frac {50}{60}\times 3 \\[ 5pt ] &=&2.5 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，回路全体のインピーダンス\( \ Z^{\prime } \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
Z^{\prime }&=&\sqrt {R^{2}+{{X_{\mathrm {C}}}^{\prime }}^{2}} \\[ 5pt ] &=&\sqrt {4^{2}+2.5^{2}} \\[ 5pt ] &≒&4.717 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，このときに流れる電流\( \ I^{\prime } \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I^{\prime }&=&\frac {E}{Z^{\prime }} \\[ 5pt ] &=&\frac {100}{4.717} \\[ 5pt ] &≒&21.2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。