《理論》〈電気回路〉[R4上:問17]誘電率の異なるコンデンサの直列接続に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

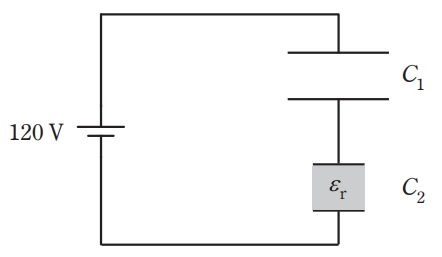
図のように直列に接続された二つの平行平板コンデンサに\( \ 120 \ \mathrm {V} \ \)の電圧が加わっている。コンデンサ\( \ C_{1} \ \)の金属板間は真空であり，コンデンサ\( \ C_{2} \ \)の金属板間には比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体が挿入されている。コンデンサ\( \ C_{1} \ \)，\( \ C_{2} \ \)の金属板間の距離は等しく，\( \ C_{1} \ \)の金属板の面積は\( \ C_{2} \ \)の\( \ 2 \ \)倍である。このとき，コンデンサ\( \ C_{1} \ \)の両端の電圧が\( \ 80 \ \mathrm {V} \ \)であった。次の(a)及び(b)の問に答えよ。

ただし，コンデンサの端効果は無視できるものとする。

(a)　コンデンサ\( \ C_{2} \ \)の誘電体の比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1 \ \)　　(2)　\( \ 2 \ \)　　(3)　\( \ 3 \ \)　　(4)　\( \ 4 \ \)　　(5)　\( \ 5 \ \)　

(b)　\( \ C_{1} \ \)の静電容量が\( \ 30 \ \mathrm {\mu F} \ \)のとき，\( \ C_{1} \ \)と\( \ C_{2} \ \)の合成容量の値\( \ \mathrm {[\mu F]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 10 \ \)　　(2)　\( \ 20 \ \)　　(3)　\( \ 30 \ \)　　(4)　\( \ 40 \ \)　　(5)　\( \ 50 \ \)　

【ワンポイント解説】

直列に接続した誘電率の異なる平行平板コンデンサに関する問題です。
直列接続する場合には，各コンデンサに蓄えられる電荷が等しくなることを利用して解くと良いです。
また，コンデンサのインピーダンスが\( \ \displaystyle \frac {1}{\mathrm {j}\omega C} \ \)であり，静電容量に反比例することを利用すれば分圧の法則等でも解くことは可能かと思います。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \)，極板の面積を\( \ S \ \)，極板間の距離を\( \ d \ \)とすると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。平行平板コンデンサの間に比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体を挿入すると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

3.コンデンサの合成静電容量
コンデンサ容量が\( \ C_{1} \ \)と\( \ C_{2} \ \)のコンデンサがある場合，直並列の合成静電容量\( \ C \ \)は下記の通りとなります。抵抗の場合と直並列が逆になることを知っておきましょう。
①並列回路の合成静電容量
\[
\begin{eqnarray}
C&=&C_{1}+C_{2} \\[ 5pt ] \end{eqnarray}
\] ②直列回路の合成静電容量
\[
\begin{eqnarray}
\frac {1}{C}&=&\frac {1}{C_{1}}+\frac {1}{C_{2}} \\[ 5pt ] \end{eqnarray}
\] 整理すると，
\[
\begin{eqnarray}
C&=&\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(4)
題意より，コンデンサ\( \ C_{1} \ \)の両端の電圧\( \ V_{1}=80 \ \mathrm {[V]} \ \)なので，コンデンサ\( \ C_{2} \ \)の両端の電圧\( \ V_{2}=40 \ \mathrm {[V]} \ \)である。蓄えらえる電荷が等しいので，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」より，
\[
\begin{eqnarray}
Q =C_{1}V_{1}&=&C_{2}V_{2} \\[ 5pt ] C_{1}\times 80&=&C_{2}\times 40 \\[ 5pt ] 2C_{1}&=&C_{2}　　　・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。また，各コンデンサの静電容量は，\( \ C_{1} \ \)の金属板の面積を\( \ S \ \)，金属板間の距離を\( \ d \ \)とすると，ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」の通り，
\[
\begin{eqnarray}
C_{1} &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] C_{2} &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}\displaystyle \frac {S}{2}}{d} \\[ 5pt ] &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{2d} \\[ 5pt ] \end{eqnarray}
\] となり，①式より，
\[
\begin{eqnarray}
2C_{1}&=&C_{2} \\[ 5pt ] 2\cdot \frac {\varepsilon _{0}S}{d}&=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{2d} \\[ 5pt ] 2&=&\frac {\varepsilon _{\mathrm {r}} }{2} \\[ 5pt ] \varepsilon _{\mathrm {r}}&=&4 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
①式に\( \ C_{1}=30 \ \mathrm {[\mu F]} \ \)を代入すれば，
\[
\begin{eqnarray}
C_{2}&=&2C_{1} \\[ 5pt ] &=&2\times 30 \\[ 5pt ] &=&60 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}
\] となるため合成静電容量\( \ C \ \mathrm {[\mu F]} \ \)は，ワンポイント解説「3.コンデンサの合成静電容量」の通り，
\[
\begin{eqnarray}
C&=&\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ] &=&\frac {30\times 60}{30+60} \\[ 5pt ] &=&20 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}
\] と求められる。