《理論》〈電磁気〉[H27:問5]三角形ループの移動による誘導起電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

十分長いソレノイド及び小さい三角形のループがある。図1はソレノイドの横断図を示しており，三角形ループも同じ面内にある。図2はその破線部分の拡大図である。面\(x=0\)から右側の領域(\(x > 0\)の領域)は直流電流を流したソレノイドの内側であり，そこには\(+z\)方向の平等磁界が存在するとする。その磁束密度を\(B \ \mathrm {[T]}\)(\(B > 0\) )とする。

一方，左側領域(\(x < 0\) )はソレノイドの外側であり磁界は零であるとする。ここで，三角形\(\mathrm {PQR}\)の抵抗器付き導体ループが\(xy\)平面内を等速度\(u \ \mathrm {[m/s]}\)で\(+x\)方向に進み，ソレノイドの巻線の隙間から内側に侵入していく。その際，導体ループの辺\(\mathrm {QR}\)は\(y\)軸と平行を保っている。頂点\(\mathrm {P}\)が面\(x = 0\)を通過する時刻を\(T \ \mathrm {[s]}\)とする。また，抵抗器の抵抗\(r \ [\Omega ] \)は十分大きいものとする。

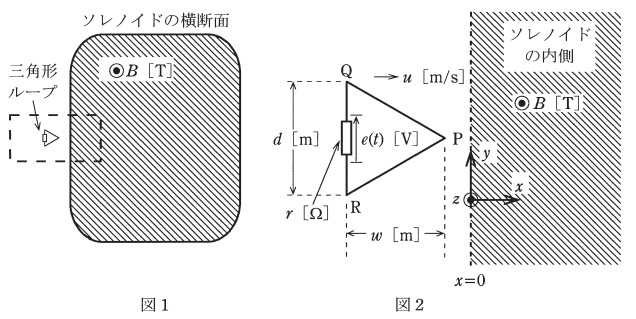
辺\(\mathrm {QR}\)の中央の抵抗器に時刻\(t \ \mathrm {[s]}\)に加わる誘導電圧を\(e ( t ) \ \mathrm {[V]}\)とし，その符号は図中の矢印の向きを正と定義する。三角形ループがソレノイドの外側から内側へ入り込むときの\(e ( t ) \)を示す図として，最も近いものを次の(1)～(5)のうちから一つ選べ。

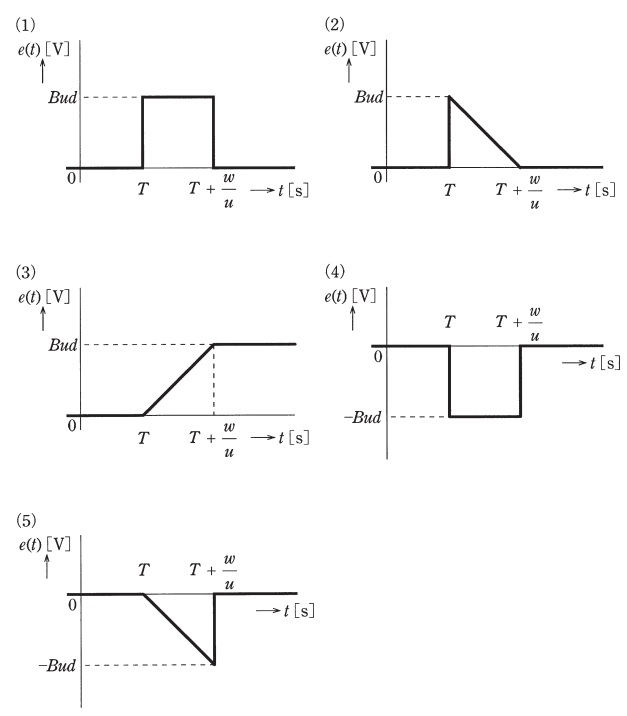
【ワンポイント解説】

誘導起電力の大きさと向きの導出がしっかりと理解できているかどうかを問う問題です。ループが三角形であることと誘導起電力の向きを定義しているところが，受験生を迷わす問題であると思います。

1.電磁誘導に関するファラデーの法則
誘導起電力の大きさ\(e\)はコイルを貫く磁束\(\phi\)の時間変化に等しいという法則で，
\[
e=-\frac {\Delta \phi }{\Delta t}
\] となります。式についている－の符号は変化する磁束を打ち消す方向に誘導起電力が発生するという意味です。
また，磁束\(\phi\)の変化量\(\Delta \phi \)は磁束密度\(B\)を一定とすると，面積変化\(\Delta S\)を用いて，
\[
\Delta \phi =B\Delta S
\] と計算できます。

【解答】

解答：(5)
題意に沿って，三角形ループの動きを描くと図3のようになる。

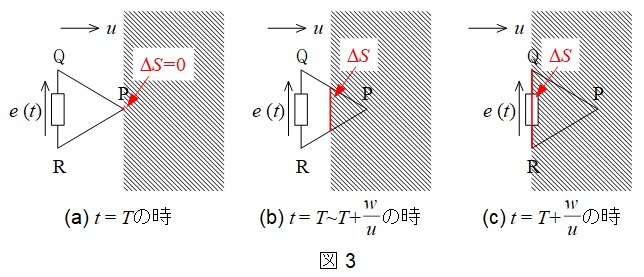
ワンポイント解説「1.電磁誘導に関するファラデーの法則」より，
\[
\begin{eqnarray}
e&=&-\frac {\Delta \phi }{\Delta t} \\[ 5pt ] &=&-B\frac {\Delta S }{\Delta t}
\end{eqnarray}
\] となる。図3の通り，\(\Delta S\)は時間の経過とともに大きくなるので，誘導起電力\(e\)の大きさも徐々に大きくなる。\(\displaystyle t=T+\frac {w}{u}\)以降は\(S\)に変化がないので，\(\Delta S=0\)となり，誘導起電力\(e\)の大きさも零となる。
また，\(\displaystyle t=T+\frac {w}{u}\)の時，
\[
\Delta S= u \Delta t d
\] となるので，その時の誘導起電力\(e\)は，
\[
\begin{eqnarray}
e&=&-\frac {\Delta \phi }{\Delta t} \\[ 5pt ] &=&-B\frac {\Delta S }{\Delta t} \\[ 5pt ] &=&-B\frac { u \Delta t d}{\Delta t} \\[ 5pt ] &=&-B u d
\end{eqnarray}
\] と求められる。また，方向は磁界の変化を打ち消す方向に誘導起電力が発生するため，\(e(t)\)はマイナスとなる。