《理論》〈電磁気〉[H26:問17]真空中の電荷に働く力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

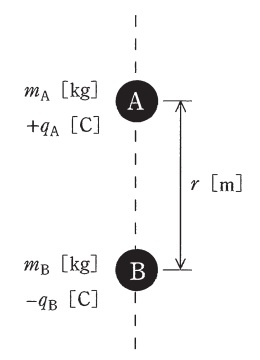
図のように，真空中において二つの小さな物体$\mathrm {A}$，$\mathrm {B}$が距離$r \ \mathrm {[m]}$を隔てて鉛直線上に置かれている。$\mathrm {A}$は固定されており，$\mathrm {A}$の真下に$\mathrm {B}$がある。物体$\mathrm {A}$，$\mathrm {B}$はそれぞれ，質量$m_{\mathrm {A}} \ \mathrm {[kg]}$，$m_{\mathrm {B}} \ \mathrm {[kg]}$をもち，電荷$+q_{\mathrm {A}} \ \mathrm {[C]}$，$-q_{\mathrm {B}} \ \mathrm {[C]}$を帯びている。$q_{\mathrm {A}} ＞ 0$，$q_{\mathrm {B}} ＞ 0$とし，真空の誘電率を$\varepsilon _{0} \ \mathrm {[F / m]}$とする。次の(a)及び(b)の問に答えよ。

ただし，小問(a)においては重力加速度$g \ \mathrm {[m / s^{2} ]}$の重力を，小問(b)においては無重力を，それぞれ仮定する。物体$\mathrm {A}$，$\mathrm {B}$の間の万有引力は無視する。

(a)　重力加速度$g \ \mathrm {[m / s^{2} ]}$の重力のもとで$\mathrm {B}$を初速度零で放ったとき，$\mathrm {B}$は$\mathrm {A}$に近づくように上昇を始めた。このときの条件を表す式として，正しいものを次の(1)～(5)のうちから一つ選べ。
$$\begin{eqnarray} &&(1)　\frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r^{2}} ＞ m_{\mathrm {B}}g　　(2)　\frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r} ＞ m_{\mathrm {B}}g　　(3)　\frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi r} ＞ m_{\mathrm {B}}g \\[ 5pt ] &&(4)　\frac {q_{\mathrm {A}}q_{\mathrm {B}}}{2\pi \varepsilon _{0} r^{2}} ＞ m_{\mathrm {B}}g　　(5)　\frac {q_{\mathrm {A}}q_{\mathrm {B}}}{2\pi \varepsilon _{0} r} ＞ m_{\mathrm {B}}g \\[ 5pt ] \end{eqnarray}$$

(b)　無重力のもとで$\mathrm {B}$を下向きの初速度$v_{\mathrm {B}} \ \mathrm {[m / s ]}$で放ったとき，$\mathrm {B}$は下降を始めたが，途中で速度の向きが変わり上昇に転じた。このときの条件を示す式として，正しいものを次の(1)～(5)のうちから一つ選べ。
$$\begin{eqnarray} &&(1)　\frac {1}{2}m_{\mathrm {B}}v_{\mathrm {B}}^{2} ＜ \frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r^{2}}　　　&(2)&　\frac {1}{2}m_{\mathrm {B}}v_{\mathrm {B}}^{2} ＜ \frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r}　　(3)　m_{\mathrm {B}}v_{\mathrm {B}} ＜ \frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r^{2}} \\[ 5pt ] &&(4)　m_{\mathrm {B}}v_{\mathrm {B}} ＜ \frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r}　　&(5)&　\frac {1}{2}m_{\mathrm {B}}v_{\mathrm {B}} ＜ \frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r^{2}} \\[ 5pt ] \end{eqnarray}$$

【ワンポイント解説】

電磁気と力学を組み合わせたような問題となっています。(a)は力の大きさ，(b)はエネルギーの大きさのバランスで条件が決まります。

1.クーロンの法則
距離$r$離れた二つの電荷$q_{\mathrm {A}}$，$q_{\mathrm {B}}$に加わる力$F$は，真空の誘電率を$\varepsilon _{0}$とすると，
$$F=\frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r^{2}}$$ となります。法則なので，覚えるのが原則となります。

【解答】

(a)解答：(1)
$\mathrm {B}$に働く重力の大きさは，$m_{\mathrm {B}} g$なので，クーロン力が重力より大きくなればよい。よって，ワンポイント解説「1.クーロンの法則」より，
$$\frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r^{2}} ＞ m_{\mathrm {B}}g$$ と求められる。

(b)解答：(2)
$\mathrm {B}$の下向きの運動エネルギーの大きさは，$\displaystyle \frac {1}{2} m_{\mathrm {B}}v_{\mathrm {B}}^{2}$であり，クーロン力による上向きのエネルギーの大きさは，
$$F\cdot r = \frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r}$$ であるから，上昇に転じる条件は，
$$\frac {1}{2}m_{\mathrm {B}}v_{\mathrm {B}}^{2} ＜ \frac {q_{\mathrm {A}}q_{\mathrm {B}}}{4\pi \varepsilon _{0} r}$$ と求められる。