【問題】
【難易度】★★★☆☆(普通)
図1は,代表的なスイッチング電源回路の原理図を示している。次の(a)及び(b)の問に答えよ。
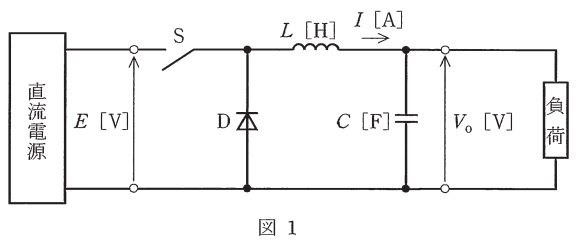
(a) 回路の説明として,誤っているものを次の(1)~(5)のうちから一つ選べ。
(1) インダクタンス\(L \ \mathrm {[H]}\)のコイルはスイッチ\(\mathrm {S}\)がオンのときに電磁エネルギーを蓄え,\(\mathrm {S}\)がオフのときに蓄えたエネルギーを放出する。
(2) ダイオード\(\mathrm {D}\)は,スイッチ\(\mathrm {S}\)がオンのときには電流が流れず,\(\mathrm {S}\)がオフのときに電流が流れる。
(3) 静電容量\(C \ \mathrm {[F]}\)のコンデンサは出力電圧\(V_{\mathrm {o}} \ \mathrm {[V]}\)を平準化するための素子であり,静電容量\(C \ \mathrm {[F]}\)が大きいほどリプル電圧が小さい。
(4) コイルのインダクタンスやコンデンサの静電容量値を小さくするためには,スイッチ\(\mathrm {S}\)がオンとオフを繰り返す周期(スイッチング周期)を長くする。
(5) スイッチの実現には,バイポーラトランジスタや電界効果トランジスタが使用できる。
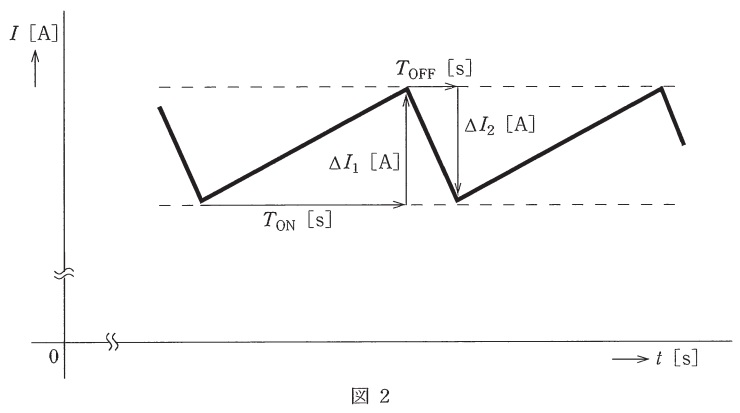
(b) スイッチ\(\mathrm {S}\)がオンの間にコイルの電流\(I\)が増加する量を\(\Delta I_{1} \ \mathrm {[A]}\)とし,スイッチ\(\mathrm {S}\)がオフの間に\(I\)が減少する量を\(\Delta I_{2} \ \mathrm {[A]}\)とすると,定常的には図2の太線に示すような電流の変化がみられ,\(\Delta I_{1}=\Delta I_{2}\)が成り立つ。
ここで出力電圧\(V_{\mathrm {o}} \ \mathrm {[V]}\)のリプルは十分に小さく,出力電圧を一定とし,電流\(I\)の増減は図2のように直線的であるとする。また,ダイオードの順方向電圧は\(0 \ \mathrm {V}\)と近似する。さらに,スイッチ\(\mathrm {S}\)がオン並びにオフしている時間をそれぞれ\(T_{\mathrm {ON}} \ \mathrm {[s]}\),\(T_{\mathrm {OFF}} \ \mathrm {[s]}\)とする。
\(\Delta I_{1}\)と\(V_{\mathrm {o}}\)を表す式の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& \Delta I_{1} & V_{\mathrm {o}} \\
\hline
(1) & \displaystyle \frac {(E-V_{o})T_{\mathrm {ON}}}{L} & \displaystyle \frac {T_{\mathrm {OFF}}E}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\
\hline
(2) & \displaystyle \frac {(E-V_{o})T_{\mathrm {ON}}}{L} & \displaystyle \frac {T_{\mathrm {ON}}E}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\
\hline
(3) & \displaystyle \frac {(E-V_{o})T_{\mathrm {ON}}}{L} & \displaystyle \frac {(T_{\mathrm {ON}}+T_{\mathrm {OFF}})E}{T_{\mathrm {OFF}}} \\
\hline
(4) & \displaystyle \frac {(V_{o}-E)T_{\mathrm {ON}}}{L} & \displaystyle \frac {(T_{\mathrm {ON}}+T_{\mathrm {OFF}})E}{T_{\mathrm {ON}}} \\
\hline
(5) & \displaystyle \frac {(V_{o}-E)T_{\mathrm {ON}}}{L} & \displaystyle \frac {(T_{\mathrm {ON}}+T_{\mathrm {OFF}})E}{T_{\mathrm {OFF}}} \\
\hline
\end{array}
\]
【ワンポイント解説】
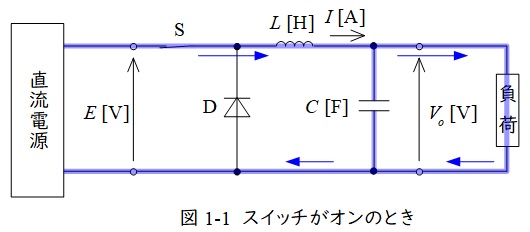
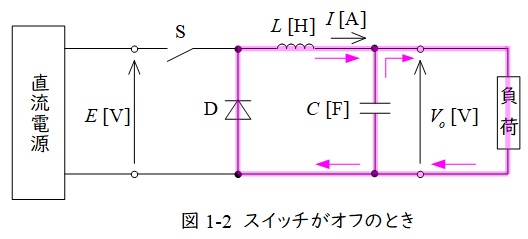
機械科目のパワーエレクトロニクスの直流チョッパのような内容の問題です。下図のようにスイッチがオンの時とオフの時で導通する場所が変わります。電圧と電流がどうなるかよく考えて理解するようにしましょう。
【関連する「電気の神髄」記事】
【解答】
(a)解答:(4)
(1):正しい
問題文の通り,リアクトル\(L\)はスイッチ\(\mathrm {S}\)がオンのときに電源からの電磁エネルギーを蓄え,スイッチ\(\mathrm {S}\)がオフのときに電磁エネルギーを放出します。
(2):正しい
ワンポイント解説図1-1,図1-2の通りダイオードはスイッチ\(\mathrm {S}\)がオンの時は電流は流れず,オフの時電流が流れます。
(3):正しい
静電容量が大きいほど,大きな電荷が蓄積されるため,電圧の変化が小さくなり,リプル(脈動)も小さくなります。
(4):誤り
スイッチ周期を長くするためには,その分十分な静電容量とインダクタンスが必要となります。したがって,コイルのインダクタンスやコンデンサの静電容量値を小さくするためには,スイッチ\(\mathrm {S}\)がオンとオフを繰り返す周期(スイッチング周期)を短くする必要があります。
(5):正しい
問題文の通り,スイッチの実現にはトランジスタを使用します。
(b)解答:(2)
図1-1において,コイルの電圧には,
\[
\begin{eqnarray}
L\frac {\Delta I}{\Delta t} &=&E-V_{\mathrm {o}} \\[ 5pt ]
\Delta I&=&\frac {E-V_{\mathrm {o}}}{L}\Delta t \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,\(\Delta I→\Delta I_{1}\),\(\Delta t→T_{\mathrm {ON}}\)を代入すると,
\[
\begin{eqnarray}
\Delta I_{1}&=&\frac {E-V_{\mathrm {o}}}{L}T_{\mathrm {ON}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
図1-2において,コイルの電圧には,
\[
\begin{eqnarray}
L\frac {\Delta I}{\Delta t} &=&V_{\mathrm {o}} \\[ 5pt ]
\Delta I&=&\frac {V_{\mathrm {o}}}{L}\Delta t \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,\(\Delta I→\Delta I_{2}\),\(\Delta t→T_{\mathrm {OFF}}\)を代入すると,
\[
\begin{eqnarray}
\Delta I_{2}&=&\frac {V_{\mathrm {o}}}{L}T_{\mathrm {OFF}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\(\Delta I_{1}=\Delta I_{2}\)であるから,
\[
\begin{eqnarray}
\frac {E-V_{\mathrm {o}}}{L}T_{\mathrm {ON}}&=&\frac {V_{\mathrm {o}}}{L}T_{\mathrm {OFF}} \\[ 5pt ]
V_{\mathrm {o}}&=&\frac {T_{\mathrm {ON}}E}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは