《理論》〈電磁気〉[H30:問17]平行平板コンデンサの誘電体挿入に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★★（難しい）

空気(比誘電率 \(1\))で満たされた極板間距離\(\ 5d \ \mathrm {[m]} \ \)の平行板コンデンサがある。図のように，一方の極板と大地との間に電圧\( \ V_{0} \ \mathrm {[V]} \ \)の直流電源を接続し，極板と同形同面積で厚さ\(\ 4d \ \mathrm {[m]} \ \)の固体誘電体(比誘電率 \(4\))を極板と接するように挿入し，他方の極板を接地した。次の(a)及び(b)の問に答えよ。

ただし，コンデンサの端効果は無視できるものとする。

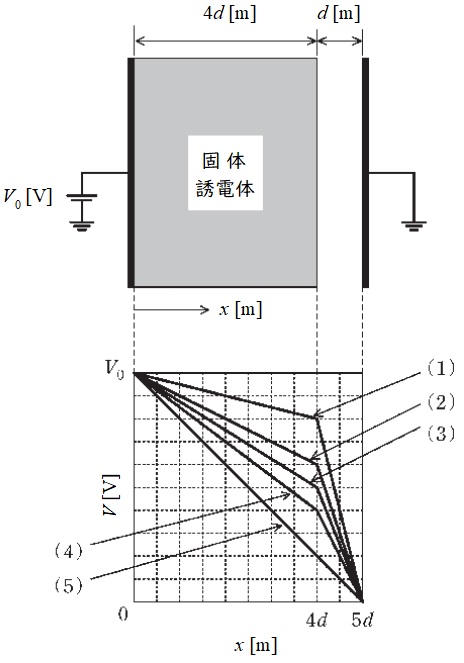
(a)　極板間の電位分布を表すグラフ(縦軸：電位\( \ V \ \mathrm {[V]} \ \)，横軸：電源が接続された極板からの距離\(\ x \ \mathrm {[m]} \ \)として，最も近いものを図中の(1)～(5)のうちから一つ選べ。

(b)　\( \ V_{0}=10 \ \mathrm {kV} \ \)，\(\ d=1 \ \mathrm {mm} \ \)とし，比誘電率 \(4\) の固体誘電体を比誘電率 \(\varepsilon _{\mathrm {r}}\)の固体誘電体に差し替え，空気ギャップの電界の強さが\( \ 2.5 \ \mathrm {kV ／ mm} \ \)となったとき，\(\varepsilon _{\mathrm {r}}\)の値として最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(0.75\)　　(2)　\(1.00\)　　(3)　\(1.33\)　　(4)　\(1.67\)　　(5)　\(2.00\)

【ワンポイント解説】

平行平板コンデンサの問題は毎年のように出題される頻出問題です。必要な公式は数種類で非常に得点源になる内容なので，確実に理解するようにしましょう。

1.平行平板コンデンサの静電容量\(C\)
比誘電率\(\varepsilon _{\mathrm {r}}\)の誘電体を挿入した時の平行平板コンデンサの静電容量\(C\)は，真空の誘電率\(\varepsilon _{0}\)，極板の面積を\(S\)，極板間の間隔を\(d\)とすると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}}\varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

2.平行平板コンデンサの電界\(E\)と電圧\(V\)の関係
平行平板コンデンサ内の電界の強さを\(E\)，極板間の電圧\(V\)，極板間隔を\(d\)とすると，
\[
\begin{eqnarray}
E &=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

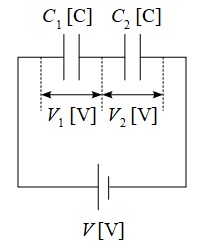
3.コンデンサにおける分圧の法則の適用
下図の示すような回路が与えられている時，各コンデンサの電圧は，
\[
\begin{eqnarray}
V_{1} &=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C_{1}}}{\displaystyle \frac {1}{\mathrm {j}\omega C_{1}}+\frac {1}{\mathrm {j}\omega C_{2}}}V \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C_{1}}}{\displaystyle \frac {\mathrm {j}\omega C_{1}+\mathrm {j}\omega C_{2}}{\mathrm {j}\omega C_{1}\cdot \mathrm {j}\omega C_{2}}}V \\[ 5pt ] &=&\frac {\mathrm {j}\omega C_{2}}{\mathrm {j}\omega C_{1}+j\omega C_{2}}V \\[ 5pt ] &=&\frac {C_{2}}{C_{1}+C_{2}}V \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
V_{2} &=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C_{2}}}{\displaystyle \frac {1}{\mathrm {j}\omega C_{1}}+\frac {1}{\mathrm {j}\omega C_{2}}}V \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C_{2}}}{\displaystyle \frac {\mathrm {j}\omega C_{1}+\mathrm {j}\omega C_{2}}{\mathrm {j}\omega C_{1}\cdot \mathrm {j}\omega C_{2}}}V \\[ 5pt ] &=&\frac {\mathrm {j}\omega C_{1}}{\mathrm {j}\omega C_{1}+\mathrm {j}\omega C_{2}}V \\[ 5pt ] &=&\frac {C_{1}}{C_{1}+C_{2}}V \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　平行平板コンデンサの静電容量まとめ

【解答】

(a)解答：(3)
ワンポイント解説「1.平行平板コンデンサの静電容量\(C\)」より，固体誘電体中の静電容量\(C_{\mathrm {r}}\)及び空気中の静電容量\(C_{0}\)は，
\[
\begin{eqnarray}
C_{\mathrm {r}} &=&\frac {\varepsilon _{\mathrm {r}}\varepsilon _{0}S}{4d} \\[ 5pt ] &=&\frac {4\varepsilon _{0}S}{4d} \\[ 5pt ] &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
C_{0} &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] &=&C_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] であるから，誘電体と空気の境界面の電位\(V\)は，ワンポイント解説「3.コンデンサにおける分圧の法則の適用」より，
\[
\begin{eqnarray}
V &=&\frac {C_{\mathrm {r}}}{C_{\mathrm {r}}+C_{0}}V_{0} \\[ 5pt ] &=&\frac {C_{0}}{C_{0}+C_{0}}V_{0} \\[ 5pt ] &=&\frac {1}{2}V_{0} \\[ 5pt ] \end{eqnarray}
\] となるので，図の(3)の通りとなる。

(b)解答：(3)
ワンポイント解説「1.平行平板コンデンサの静電容量\(C\)」より，固体誘電体中の静電容量\(C_{\mathrm {r}}^{\prime }\)は，
\[
\begin{eqnarray}
C_{\mathrm {r}}^{\prime } &=&\frac {\varepsilon _{\mathrm {r}}\varepsilon _{0}S}{4d} \\[ 5pt ] \end{eqnarray}
\] であるから，誘電体と空気の境界面の電位\(V^{\prime }\)は，
\[
\begin{eqnarray}
V^{\prime } &=&\frac {C_{\mathrm {r}}^{\prime }}{C_{\mathrm {r}}^{\prime }+C_{0}}V_{0} \\[ 5pt ] &=&\frac {\displaystyle \frac {\varepsilon _{\mathrm {r}}\varepsilon _{0}S}{4d}}{\displaystyle \frac {\varepsilon _{\mathrm {r}}\varepsilon _{0}S}{4d}+\frac {\varepsilon _{0}S}{d}}V_{0} \\[ 5pt ] &=&\frac {\displaystyle \frac {\varepsilon _{\mathrm {r}}}{4}}{\displaystyle \frac {\varepsilon _{\mathrm {r}}}{4}+1}V_{0} \\[ 5pt ] &=&\frac {\varepsilon _{\mathrm {r}}}{\varepsilon _{\mathrm {r}}+4}V_{0} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「2.平行平板コンデンサの電界\(E\)と電圧\(V\)の関係」より，
\[
\begin{eqnarray}
E &=&\frac {V^{\prime }}{d} \\[ 5pt ] V^{\prime } &=&Ed \\[ 5pt ] \frac {\varepsilon _{\mathrm {r}}}{\varepsilon _{\mathrm {r}}+4}V_{0} &=&Ed \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
\frac {\varepsilon _{\mathrm {r}}}{\varepsilon _{\mathrm {r}}+4}\times 10 &=&2.5\times 1 \\[ 5pt ] 4\varepsilon _{\mathrm {r}} &=&\varepsilon _{\mathrm {r}}+4 \\[ 5pt ] \varepsilon _{\mathrm {r}} &≒& 1.33 \\[ 5pt ] \end{eqnarray}
\] と求められる。