【問題】
【難易度】★☆☆☆☆(易しい)
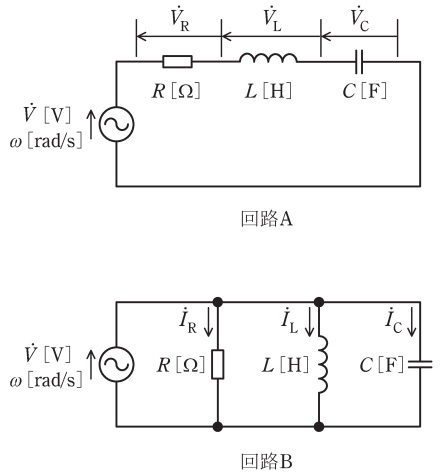
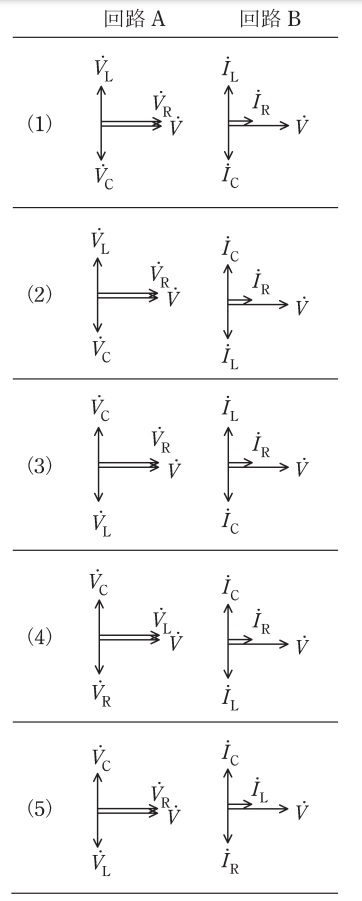
図のように,\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗,インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイル,静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサと電圧\( \ \dot V \ \mathrm {[V]} \ \),角周波数\( \ \omega \ \mathrm {[rad/s]} \ \)の交流電源からなる二つの回路\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)がある。両回路においてそれぞれ\( \ \omega ^{2}LC=1 \ \)が成り立つとき,各回路における図中の電圧ベクトルと電流ベクトルの位相の関係として,正しいものの組合せを次の(1)~(5)のうちから一つ選べ。ただし,ベクトル図における進み方向は反時計回りとする。
【ワンポイント解説】
交流回路の各インピーダンスにおける電圧と電流の関係が分かっていれば難なく解ける問題かと思います。直列回路の場合は各インピーダンスに流れる電流の大きさが等しく,並列回路の場合は各インピーダンスにかかる電圧の大きさが等しいことを理解しておきましょう。
1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンスは,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,それぞれの電圧と電流の関係は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ]
{\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ]
{\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ]
\end{eqnarray}
\]
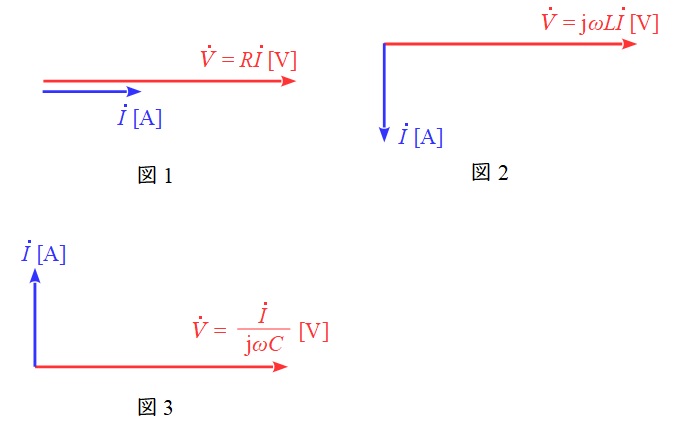
となります。この関係をベクトル図に表すと,図1~図3となります。
【関連する「電気の神髄」記事】
【解答】
解答:(2)
題意より,\( \ \omega ^{2}LC=1 \ \)すなわち\( \ \displaystyle \omega L=\frac {1}{\omega C} \ \)が成立するので進み無効電流と遅れ無効電流が打ち消し合い,回路\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)ともに,電源電圧\( \ \dot V \ \)及び電源を流れる電流\( \ \dot I \ \)の位相が同相となる。
したがって,回路\( \ \mathrm {A} \ \)は直列回路であるから,各素子を流れる電流の大きさが等しいので,ワンポイント解説「1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」に沿ってベクトル図を描くと図4のようになる。
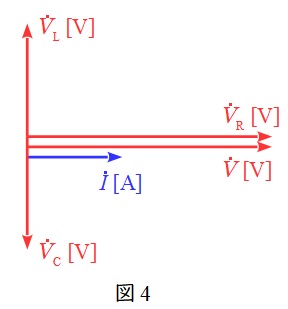
一方,回路\( \ \mathrm {B} \ \)は並列回路であるから,各素子かかる電圧が等しいため,ワンポイント解説「1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」に沿ってベクトル図を描くと図5のようになる。
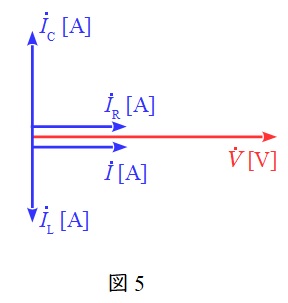
以上から,回路\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)のベクトル図の関係を満たすのは(2)となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは