《機械》〈同期機〉[H21:問5]三相同期発電機の短絡比の導出に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

定格出力\( \ 5 \ 000 \ \mathrm {[kV\cdot A]} \ \)，定格電圧\( \ 6 \ 600 \ \mathrm {[V]} \ \)の三相同期発電機がある。無負荷時に定格電圧となる励磁電流に対する三相短絡電流（持続短絡電流）は，\( \ 500 \ \mathrm {[A]} \ \)であった。この同期発電機の短絡比の値として，最も近いのは次のうちどれか。

　(1)　\( \ 0.660 \ \)　　(2)　\( \ 0.875 \ \)　　(3)　\( \ 1.00 \ \)　　(4)　\( \ 1.14 \ \)　　(5)　\( \ 1.52 \ \)

【ワンポイント解説】

三相同期発電機の短絡比を求める問題です。
短絡比の定義式を知っていれば，三相短絡電流が与えられていますので，あとは定格電流を求めるだけであることが想像つくかと思います。

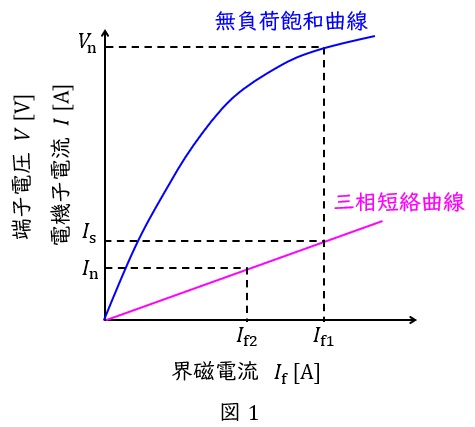
1.同期発電機の無負荷飽和曲線と三相短絡曲線
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。図中の\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)は定格電圧，\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は定格電流，三相短絡曲線は曲線ですが，ほぼ比例の直線と近似できます。
この時，\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は定格電圧時の三相短絡電流であり，短絡比\( \ K \ \)は，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
本問の同期発電機の定格電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，定格容量が\( \ P_{\mathrm {n}}=5 \ 000 \ \mathrm {[kV\cdot A]} \ \)，定格電圧が\( \ V_{\mathrm {n}}=6 \ 600 \ \mathrm {[V]} \ \)であるから，
\[
\begin{eqnarray}
I_{\mathrm {n}} &=& \frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=& \frac {5 \ 000\times 10^{3}}{\sqrt {3}\times 6 \ 600} \\[ 5pt ] &≒&437.4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，三相短絡電流\( \ I_{\mathrm {s}}=500 \ \mathrm {[A]} \ \)より短絡比\( \ K \ \)は，ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通り，
\[
\begin{eqnarray}
I_{\mathrm {s}} &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ] &=& \frac {500}{437.4} \\[ 5pt ] &≒&1.14 \\[ 5pt ] \end{eqnarray}
\] と求められる。