《機械》〈パワーエレクトロニクス〉[R2:問16]単相インバータで交流を給電する回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

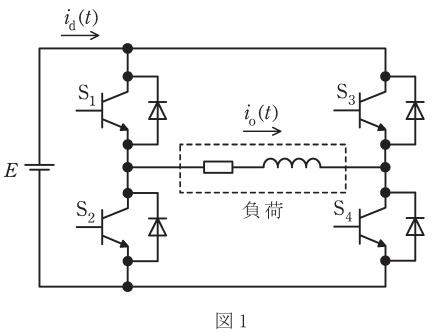
図1は，直流電圧源から単相インバータで誘導性負荷に交流を給電する基本回路を示す。負荷電流\( \ i_{\mathrm {o}}\left( t \right) \ \)と直流側電流\( \ i_{\mathrm {d}}\left( t \right) \ \)は図示する矢印の向きを正の方向として，次の(a)及び(b)の問に答えよ。

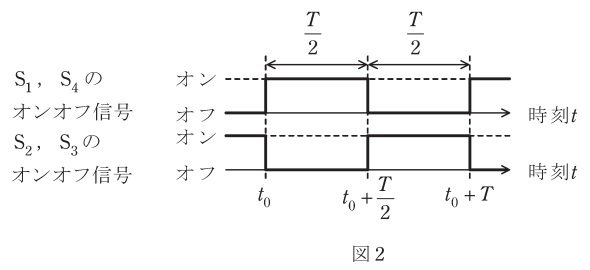
(a)　各パワートランジスタが出力交流電圧の\( \ 1 \ \)周期\( \ T \ \)に\( \ 1 \ \)回オンオフする運転を行っている際のある時刻\( \ t_{\mathrm {0}} \ \)から\( \ 1 \ \)周期の波形を図2に示す。直流電圧が\( \ E \ \mathrm {[V]} \ \)のとき，交流側の方形波出力電圧の実効値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.5E \ \)　　(2)　\( \ 0.61E \ \)　　(3)　\( \ 0.86E \ \)　　(4)　\( \ E \ \)　　(5)　\( \ 1.15E \ \)

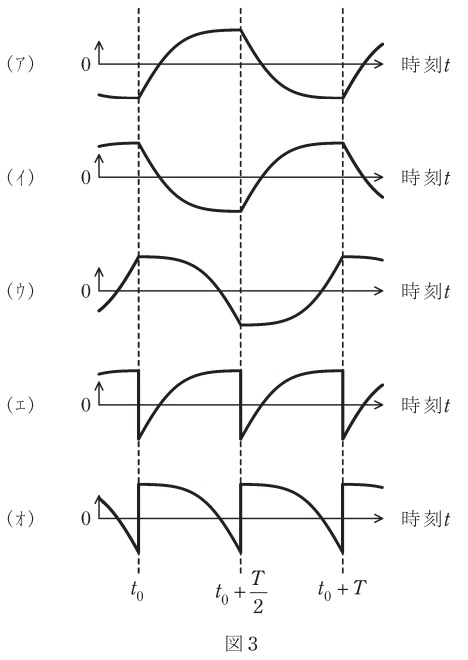
(b)　小問(a)のとき，負荷電流\( \ i_{\mathrm {o}}\left( t \right) \ \)の波形が図3の（ア）～（ウ），直流側電流\( \ i_{\mathrm {d}}\left( t \right) \ \)の波形が図3の（エ），（オ）のいずれかに示されている。それらの波形の適切な組合せを次の(1)～(5)のうちから一つ選べ。

　(1)　（ア）と（エ）　　(2)　（イ）と（エ）　　(3)　（ウ）と（オ）
　(4)　（ア）と（オ）　　(5)　（イ）と（オ）　

【ワンポイント解説】

方形波の実効値及び単相インバータのメカニズムを理解していないと解けない問題です。
あまり出題されない方形波の実効値の内容もあるので★５か迷いましたが，平成24年に(b)と同様な問題があるので，★４としました。３種としては難易度が高い問題であると思います。

1.方形波の平均値及び実効値
方形波の平均値及び実効値は以下のように求められます。いずれも積分計算を伴うので３種受験時には結果を覚えていれば問題ありません。
①平均値
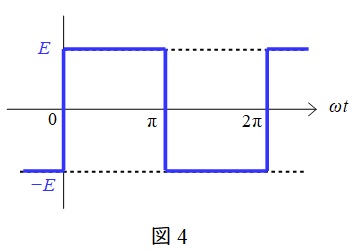
瞬時値が図4で表される方形波の平均値\( \ E_{\mathrm {av}} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {av}} &=& \frac {1}{\pi}\int ^{\pi}_{0} E \mathrm {d}\left( \omega t\right) \\[ 5pt ] &=& \frac {E}{\pi}\left[ \omega t \right] ^{\pi}_{0} \\[ 5pt ] &=& \frac {E}{\pi}\left( \pi \right) \\[ 5pt ] &=& E \\[ 5pt ] \end{eqnarray}
\] と求められます。

②実効値
瞬時値が図4で表される方形波の実効値\( \ E_{\mathrm {e}} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {e}} &=& \sqrt {\frac {1}{2\pi} \left\{ \int ^{\pi}_{0}E^{2}\mathrm {d}\left( \omega t\right) +\int ^{2\pi}_{\pi}\left( -E\right) ^{2}\mathrm {d}\left( \omega t\right) \right\} } \\[ 5pt ] &=& \sqrt {\frac {E^{2}}{2\pi} \left\{ \int ^{\pi}_{0} \mathrm {d}\left( \omega t\right) +\int ^{2\pi}_{\pi} \mathrm {d}\left( \omega t\right) \right\} } \\[ 5pt ] &=&\sqrt {\frac {E^{2}}{2\pi}\left( \pi-0+2\pi -\pi \right) } \\[ 5pt ] &=& \sqrt {E^{2}} \\[ 5pt ] &=& E \\[ 5pt ] \end{eqnarray}
\] と求められます。

【関連する「電気の神髄」記事】

　　単相電圧形フルブリッジインバータ

【解答】

(a)解答：(4)
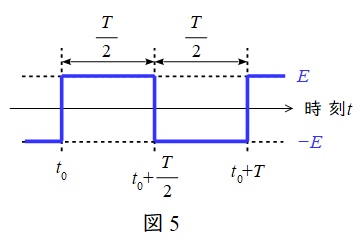
\( \ \mathrm {S}_{\mathrm {1}} \ \)及び\( \ \mathrm {S}_{\mathrm {4}} \ \)がONのとき，負荷にかかる電圧は正の電圧であり，\( \ \mathrm {S}_{\mathrm {2}} \ \)及び\( \ \mathrm {S}_{\mathrm {3}} \ \)がONのとき，負荷にかかる電圧は負の電圧である。したがって，出力電圧は図5のようになる。
ワンポイント解説「1.方形波の平均値及び実効値」の通り，最大値が\( \ E \ \mathrm {[V]} \ \)の方形波の実効値は\( \ E \ \mathrm {[V]} \ \)と求められる。

(b)解答：(1)
パワートランジスタの各状態が変化した時の電流の流れを図1-1～図1-4に示す。
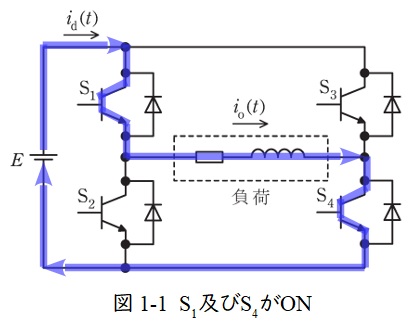
まず，\( \ \mathrm {S}_{1} \ \)と\( \ \mathrm {S}_{4} \ \)がONとなり，十分時間が経過すると，図1-1のように電流が流れる。
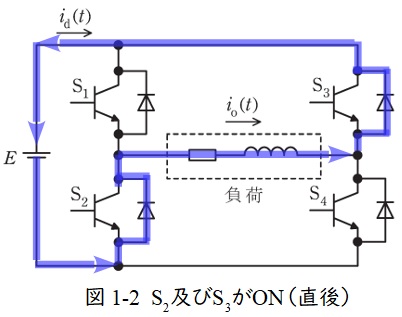
次に，\( \ \mathrm {S}_{1} \ \)と\( \ \mathrm {S}_{4} \ \)がOFFとなり，\( \ \mathrm {S}_{2} \ \)と\( \ \mathrm {S}_{3} \ \)がONになると，図1-2のように，リアクトルに蓄えられているエネルギーが消費され，電流が還流ダイオードを流れ，電源に戻るような流れとなる。
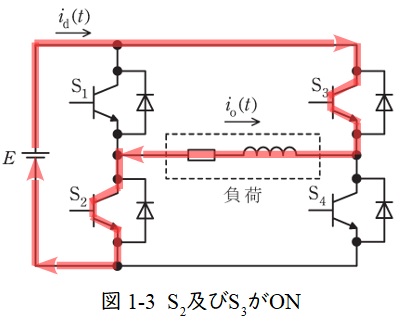
その後，時間が経過すると，図1-3のように\( \ \mathrm {S}_{2} \ \)と\( \ \mathrm {S}_{3} \ \)のパワートランジスタを電流が流れ，負荷に流れる電流の向きが逆向きになる。
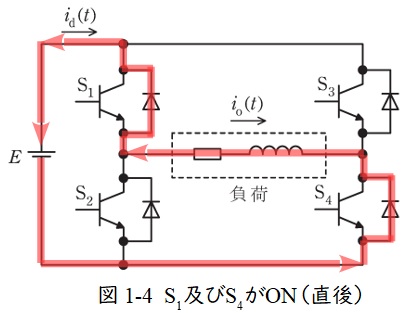
再び，\( \ \mathrm {S}_{2} \ \)と\( \ \mathrm {S}_{3} \ \)がOFFとなり，\( \ \mathrm {S}_{1} \ \)と\( \ \mathrm {S}_{4} \ \)がONになると，図1-4のように，リアクトルに蓄えられているエネルギーが消費され，電流が還流ダイオードを流れ，電源に戻るような流れとなる。その後，図1-1のようになり，以後繰り返す。