Contents
【問題】
【難易度】★★★★☆(やや難しい)
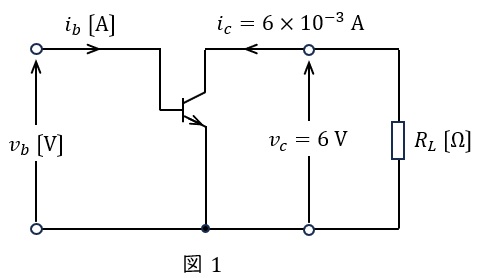
図1の回路は,エミッタ接地のトランジスタ増幅器の交流小信号に注目した回路である。次の(a)及び(b)に答えよ。
ただし,\( \ R_{L} \ \mathrm {[\Omega]} \ \)は抵抗,\( \ i_{b} \ \mathrm {[A]} \ \)は入力信号電流,\( \ i_{c}=6\times 10^{-3} \ \mathrm {[A]} \ \)は出力信号電流,\( \ v_{b} \ \mathrm {[V]} \ \)は入力信号電圧,\( \ v_{c}=6 \ \mathrm {[V]} \ \)は出力信号電圧である。
(a) 図1の回路において,入出力信号の関係を表1に示す\( \ h \ \)パラメータを用いて表すと次の式①,②になる。
\[
\begin{eqnarray}
v_{b}&=&h_{ie}i_{b}+h_{re}v_{c} &・・・・・・・・・・ ①& \\[ 5pt ]
i_{c}&=&h_{fe}i_{b}+h_{oe}v_{c} &・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
\[
表 \ 1 h \ パラメータの数値例 \\
\begin{array}{|c|c|c|}
\hline
名 称 & 記 号 & 値の例 \\
\hline
\ \fbox { (ア) } \ & h_{ie} & 3.5\times 10^{3} \ \mathrm {[\Omega]} \\
\hline
電圧帰還率 & \ \fbox { (ウ) } \ & 1.3\times 10^{-4} \\
\hline
電流増幅率 & \ \fbox { (エ) } \ & 140 \\
\hline
\ \fbox { (イ) } \ & h_{oe} & 9\times 10^{-6} \ \mathrm {[S]} \\
\hline
\end{array}
\]
上記表中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 入力インピーダンス & 出力アドミタンス & h_{fe} & h_{re} \\
\hline
(2) & 入力コンダクタンス & 出力インピーダンス & h_{fe} & h_{re} \\
\hline
(3) & 出力コンダクタンス & 入力インピーダンス & h_{re} & h_{fe} \\
\hline
(4) & 出力インピーダンス & 入力コンダクタンス & h_{re} & h_{fe} \\
\hline
(5) & 入力インピーダンス & 出力アドミタンス & h_{re} & h_{fe} \\
\hline
\end{array}
\]
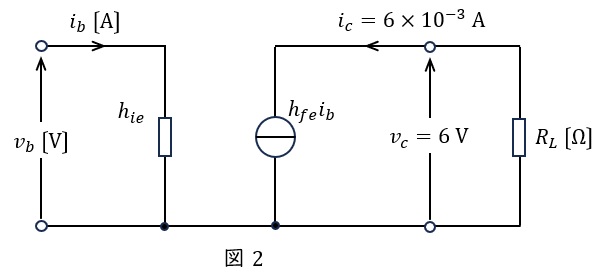
(b) 図1の回路の計算は,図2の簡易小信号等価回路を用いて行うことが多い。この場合,上記(a)の式①,②から求めた\( \ v_{b} \ \mathrm {[V]} \ \)及び\( \ i_{b} \ \mathrm {[A]} \ \)の値をそれぞれ真の値としたとき,図2の回路から求めた\( \ v_{b} \ \mathrm {[V]} \ \)及び\( \ i_{b} \ \mathrm {[A]} \ \)の誤差\( \ \Delta v_{b} \ \mathrm {[mV]} \ \),\( \ \Delta i_{b} \ \mathrm {[\mu A]} \ \)の大きさとして,最も近いものを組み合わせたのは次のうちどれか。
ただし,\( \ h \ \)パラメータの値は表1に示された値とする。
\[
\begin{array}{ccc}
& \Delta v_{b} & \Delta i_{b} \\
\hline
(1) & 0.78 & 54 \\
\hline
(2) & 0.78 & 6.5 \\
\hline
(3) & 0.57 & 6.5 \\
\hline
(4) & 0.57 & 0.39 \\
\hline
(5) & 0.35 & 0.39 \\
\hline
\end{array}
\]
【ワンポイント解説】
エミッタ接地のバイポーラトランジスタの小信号等価回路に関する問題です。
小信号等価回路は電験においては与えられるので,覚える必要はありませんが,回路計算の仕方は理解する必要があります。
そもそもなぜ小信号等価回路がこのように描けるか等は電子回路理論の学習をしっかりと行う必要がありますので,電験対策としてはそういうものだぐらいに思っておくと良いでしょう。
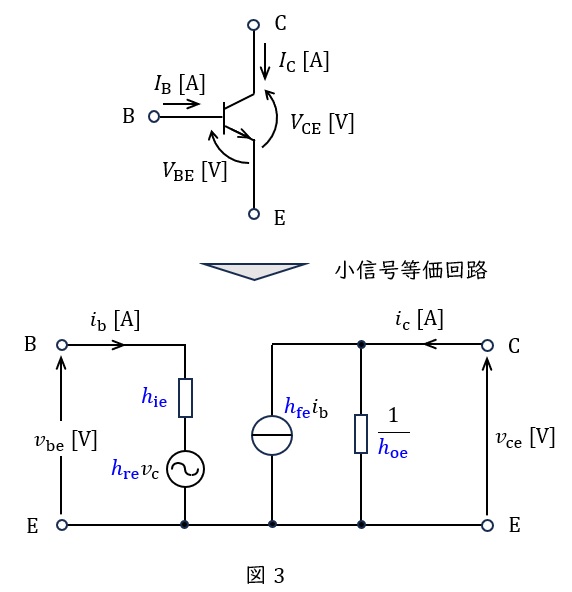
1.バイポーラトランジスタの小信号等価回路
エミッタ接地におけるバイポーラトランジスタの交流信号分に着目した小信号等価回路は図3のように描けます。入出力信号の関係を式で表すと,
\[
\begin{eqnarray}
v_{\mathrm {b}}&=&h_{\mathrm {ie}}i_{\mathrm {b}}+h_{\mathrm {re}}v_{\mathrm {c}} \\[ 5pt ]
i_{\mathrm {c}}&=&h_{\mathrm {fe}}i_{\mathrm {b}}+h_{\mathrm {oe}}v_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となりまず。ただし,\( \ h_{\mathrm {ie}} \ \),\( \ h_{\mathrm {re}} \ \),\( \ h_{\mathrm {fe}} \ \),\( \ h_{\mathrm {oe}} \ \)を\( \ h \ \)パラメータといい,
\( \ h_{\mathrm {ie}} \ \):入力インピーダンス\( \ \mathrm {[\Omega]} \ \)
\( \ h_{\mathrm {re}} \ \):電圧帰還率
\( \ h_{\mathrm {fe}} \ \):電流増幅率
\( \ h_{\mathrm {oe}} \ \):出力アドミタンス
といいます。ただし,\( \ h_{\mathrm {re}} \ \)及び\( \ h_{\mathrm {oe}} \ \)は非常に小さい値ということで無視する場合が多いです。
【解答】
(a)解答:(5)
(ア)
ワンポイント解説「1.バイポーラトランジスタの小信号等価回路」の通り,\( \ h_{ie} \ \)は入力インピーダンスとなります。単位が\( \ \mathrm {[\Omega]} \ \)なのでインピーダンスと判断すれば十分です。
(イ)
ワンポイント解説「1.バイポーラトランジスタの小信号等価回路」の通り,\( \ h_{oe} \ \)は出力アドミタンスとなります。単位が\( \ \mathrm {[S]} \ \)なのでアドミタンスと判断すれば十分です。
(ウ)
ワンポイント解説「1.バイポーラトランジスタの小信号等価回路」の通り,電圧帰還率は\( \ h_{re} \ \)となります。
(エ)
ワンポイント解説「1.バイポーラトランジスタの小信号等価回路」の通り,電流増幅率は\( \ h_{fe} \ \)となります。
(b)解答:(4)
式①,②から求めた真の値を\( \ v_{bt} \ \mathrm {[V]} \ \)及び\( \ i_{bt} \ \mathrm {[A]} \ \)とする。②式を\( \ i_{bt} \ \)について整理し,各値を代入すると,
\[
\begin{eqnarray}
i_{c}&=&h_{fe}i_{bt}+h_{oe}v_{c} \\[ 5pt ]
h_{fe}i_{bt}&=&i_{c}-h_{oe}v_{c} \\[ 5pt ]
i_{bt}&=&\frac {6\times 10^{-3}-9\times 10^{-6}\times 6}{140} \\[ 5pt ]
&≒&4.2471\times 10^{-5} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを①式に代入すると,
\[
\begin{eqnarray}
v_{bt}&=&h_{ie}i_{bt}+h_{re}v_{c} \\[ 5pt ]
&=&3.5\times 10^{3}\times 4.2471\times 10^{-5}+1.3\times 10^{-4}\times 6 \\[ 5pt ]
&≒&0.14943 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,図2より等価回路上の値\( \ v_{ba} \ \mathrm {[V]} \ \)及び\( \ i_{ba} \ \mathrm {[A]} \ \)とする。等価回路より,
\[
\begin{eqnarray}
i_{c}&=&h_{fe}i_{ba} \\[ 5pt ]
i_{ba}&=&\frac {i_{c}}{h_{fe}} \\[ 5pt ]
&=&\frac {6\times 10^{-3}}{140} \\[ 5pt ]
&≒&4.2857\times 10^{-5} \ \mathrm {[A]} \\[ 5pt ]
v_{ba}&=&h_{ie}i_{ba} \\[ 5pt ]
&=&3.5\times 10^{3}\times 4.2857\times 10^{-5} \\[ 5pt ]
&≒&0.15000 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,誤差\( \ \Delta v_{b} \ \mathrm {[mV]} \ \),\( \ \Delta i_{b} \ \mathrm {[\mu A]} \ \)は,
\[
\begin{eqnarray}
\Delta v_{b}&=&\left| v_{ba}-v_{bt}\right| \\[ 5pt ]
&=&\left| 0.15000-0.14943\right| \\[ 5pt ]
&=&0.00057 \ \mathrm {[V]} → 0.57 \ \mathrm {[mV]} \\[ 5pt ]
\Delta i_{b}&=&\left| i_{ba}-i_{bt}\right| \\[ 5pt ]
&=&\left| 4.2857\times 10^{-5}-4.2471\times 10^{-5}\right| \\[ 5pt ]
&=&0.0386\times 10^{-5} \ \mathrm {[A]} → 0.39 \ \mathrm {[\mu A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは