《理論》〈電気回路〉[H23:問16]LC回路における振動電流の波形，最大値及び周期に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図のように，電圧\( \ 100 \ \mathrm {[V]} \ \)に充電された静電容量\( \ C=300 \ \mathrm {[\mu F]} \ \)のコンデンサ，インダクタンス\( \ L=30 \ \mathrm {[mH]} \ \)のコイル，開いた状態のスイッチ\( \ \mathrm {S} \ \)からなる回路がある。時刻\( \ t=0 \ \mathrm {[s]} \ \)でスイッチ\( \ \mathrm {S} \ \)を閉じてコンデンサに充電された電荷を放電すると，回路には振動電流\( \ i \ \mathrm {[A]} \ \)（図の矢印の向きを正とする）が流れる。このとき，次の(a)及び(b)の問に答えよ。

ただし，回路の抵抗は無視できるものとする。

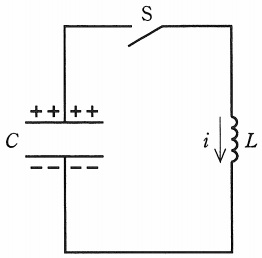
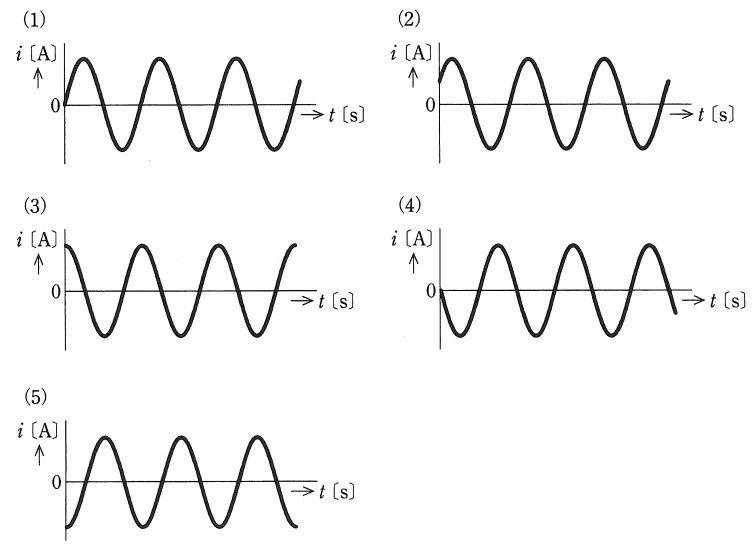
(a)　振動電流\( \ i \ \mathrm {[A]} \ \)の波形を示す図として，正しいものを次の(1)～(5)のうちから一つ選べ。

(b)　振動電流の最大値\( \ \mathrm {[A]} \ \)及び周期\( \ \mathrm {[ms]} \ \)の値の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cll}
& 　最大値　 & 　周　期　 \\
\hline
(1) & 　1.0　 & 　18.8　 \\
\hline
(2) & 　1.0　 & 　188　 \\
\hline
(3) & 　10.0　 & 　1.88　 \\
\hline
(4) & 　10.0　 & 　18.8　 \\
\hline
(5) & 　10.0　 & 　188　 \\
\hline
\end{array}
\]

【ワンポイント解説】

共振現象と過渡現象の考え方を組み合わせたようなやや発展的な問題です。
計算量は多くないですが，考え方はよく理解しておくようにしましょう。

1.直列回路の共振回路
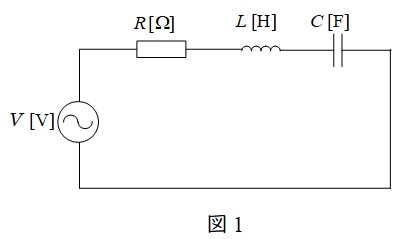
図1のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right)
\end{eqnarray}
\] となり，インピーダンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}}
\end{eqnarray}
\] となります。

2.並列回路の共振回路
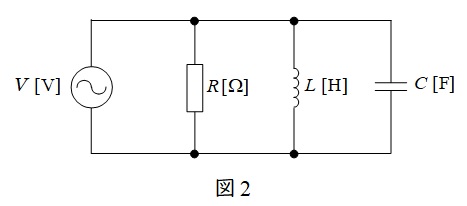
図2のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\] となり，アドミタンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}}
\end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}}
\end{eqnarray}
\] となります。

3.平行平板コンデンサの静電エネルギー\( \ W \ \)
静電容量\( \ C \ \)のコンデンサに電圧\( \ V \ \)をかけ，十分時間が経過した時にコンデンサに蓄えられる静電エネルギー\( \ W \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ Q=CV \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

4.コイルに蓄えられるエネルギー\( \ W \ \)
インダクタンス\( \ L \ \)のコイルに電流\( \ I \ \)を流し，十分時間が経過したときに蓄えられるエネルギー\( \ W \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}LI^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(1)
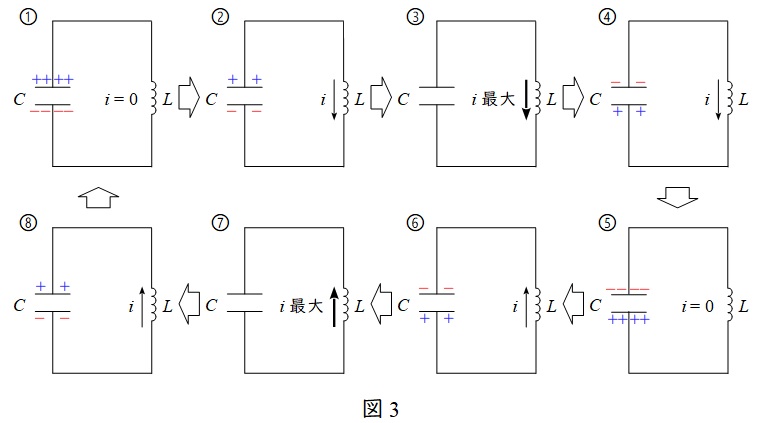
スイッチ\( \ \mathrm {S} \ \)を入れた後の電流と電荷の時間経過を図3に示す。定性的なフローは以下の通り。
①　スイッチ\( \ \mathrm {S} \ \)を入れた直後はリアクトルに逆起電力が発生し，ほとんど電流は流れないので電流は零となる。
②　時間が経過するとともに，コンデンサから電荷が放出され電流が徐々に大きくなる。
③　コンデンサに蓄えられる電荷が零のとき，電流が最大となる。
④　コンデンサに電荷が蓄えられ，電流が徐々に小さくなる。
⑤　コンデンサに電荷が①と同量蓄えられた状態になると，電流が零となる。
⑥～⑧　②～④と逆極性で同様の事象を起こす。
以降，繰り返す。

したがって，電流の波形としては(1)が適当となる。

(b)解答：(4)
図3において，エネルギー保存則により，①でコンデンサに蓄えられるエネルギーと③でリアクトルに蓄えられるエネルギーは等しいので，③で流れる電流の大きさを\( \ I_{\mathrm {m}} \ \)とすると，
\[
\begin{eqnarray}
\frac {1}{2}CV^{2} &=&\frac {1}{2}LI_{\mathrm {m}}^{2} \\[ 5pt ] CV^{2} &=&LI_{\mathrm {m}}^{2} \\[ 5pt ] I_{\mathrm {m}}^{2} &=&\frac {C}{L}V^{2} \\[ 5pt ] I_{\mathrm {m}} &=&\sqrt {\frac {C}{L}}V \\[ 5pt ] &=&\sqrt {\frac {300\times 10^{-6}}{30\times 10^{-3}}}\times 100 \\[ 5pt ] &=&\sqrt {10^{-2}}\times 100 \\[ 5pt ] &=&10^{-1}\times 100 \\[ 5pt ] &=&10 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。
問題図は並列共振回路なので，共振周波数\( \ f_{\mathrm {c}} \ \)は，ワンポイント解説「2.並列回路の共振回路」より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となり，周期\( \ T \ \)は周波数の逆数であるから，
\[
\begin{eqnarray}
T &=& \frac {1}{f_{\mathrm {c}}} \\[ 5pt ] &=& 2\pi \sqrt {LC} \\[ 5pt ] &=& 2\pi \sqrt { \left( 30\times 10^{-3}\right) \times \left( 300\times 10^{-6}\right) } \\[ 5pt ] &=& 2\pi \sqrt {9\times 10^{-6}} \\[ 5pt ] &=& 2\pi \times 3\times 10^{-3} \\[ 5pt ] &≒& 0.0188 \ \mathrm {[s]}　→　18.8 \ \mathrm {[ms]} \\[ 5pt ] \end{eqnarray}
\] と求められる。