《理論》〈電子理論〉[H25:問18]非安定マルチバイブレータに関する論説問題

【問題】

【難易度】★★★★☆（やや難しい）

図は，\( \ \mathrm {NOT} \ \mathrm {IC} \ \)，コンデンサ\( \ \mathrm {C} \ \)及び抵抗を用いた非安定マルチバイブレータの原理図である。次の(a)及び(b)の問に答えよ。

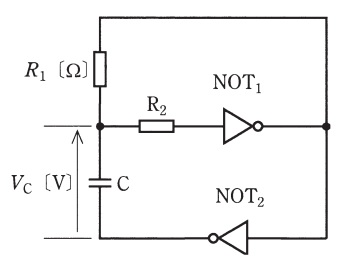
(a)　この回路に関する三つの記述(ア)～(ウ)について，正誤の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

(ア)　この回路は電源を必要としない。
(イ)　抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)の値を大きくすると，発振周波数は高くなる。
(ウ)　抵抗器\( \ \mathrm {R}_{2} \ \)は，\( \ \mathrm {NOT}_{1} \ \)に流れる入力電流を制限するための素子である。
\[
\begin{array}{cccc}
　　 & 　（ア）　 & 　（イ）　 & 　（ウ）　 \\
\hline
(1) & 正 & 正 & 正 \\
\hline
(2) & 正 & 正 & 誤 \\
\hline
(3) & 正 & 誤 & 誤 \\
\hline
(4) & 誤 & 正 & 誤 \\
\hline
(5) & 誤 & 誤 & 正 \\
\hline
\end{array}
\]

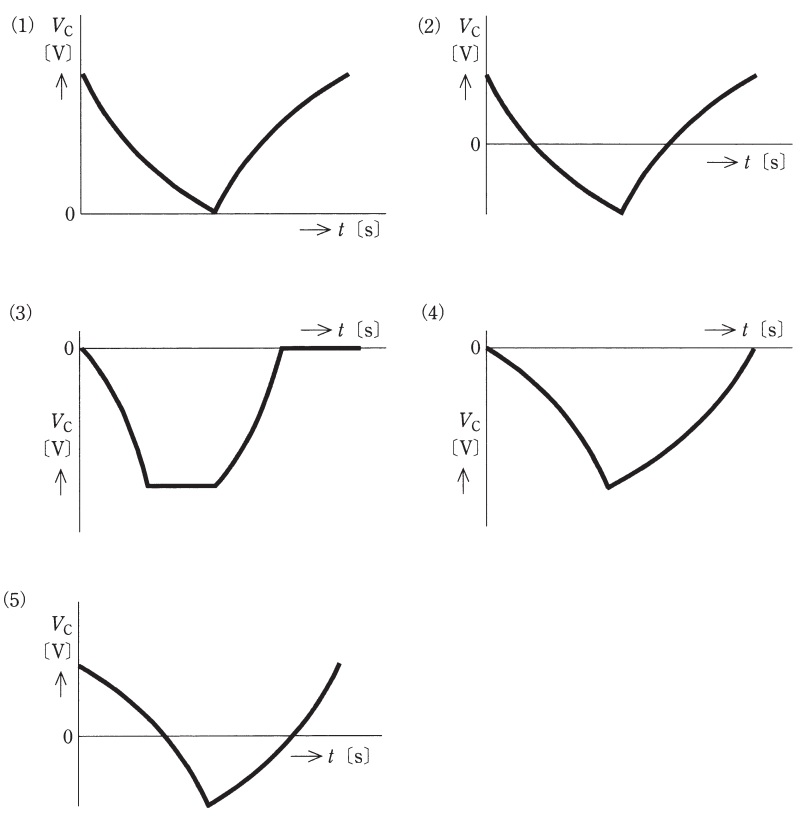
(b)　次の波形の中で，コンデンサ\( \ \mathrm {C} \ \)の端子間電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)の時間\( \ t \ \mathrm {[s]} \ \)の経過による変化の特徴を最もよく示している図として，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，いずれの図も\( \ 1 \ \)周期分のみを示している。

【ワンポイント解説】

問17と比べるとかなり難しい問題と言えると思います。コンデンサの過渡現象での振る舞いと\( \ \mathrm {NOT} \ \)素子の動作を理解している必要があります。

1.\( \ RC \ \)直列回路の過渡現象
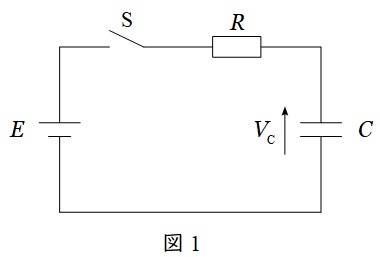
図1のような抵抗\( \ R \ \)とコンデンサ\( \ C \ \)の直列回路において，\( \ t=0 \ \)にてスイッチ\( \ \mathrm {S} \ \)を閉じた時，コンデンサの端子電圧\( \ V_{\mathrm {C}} \ \)は図2のようになります。
イメージとしては，当初電荷が貯まりやすい状態のコンデンサがあり，電圧が上がりやすく，時間が経過するとともに，コンデンサの容量の限界まで近づいていき，電圧が落ち着いていくようなイメージです。

【解答】

(a)解答：(5)
(ア)誤り
\( \ \mathrm {IC} \ \)素子は電源を必要とします。

(イ)誤り
\( \ RC \ \)直列回路の時定数は\( \ T=RC \ \)で表され，発振周波数は\( \ \displaystyle f=\frac {1}{T}=\frac {1}{RC} \ \)で表されます。本問の回路においては，発振周波数は\( \ \displaystyle f=\frac {1}{R_{1}C} \ \)で表され，発振周波数は\( \ R_{1} \ \)に反比例し，\( \ R_{1} \ \)が大きくなると発振周波数は低くなります。

(ウ)正しい
\( \ \mathrm {NOT} \ \mathrm {IC} \ \)は電源のプラスとマイナスの極性が入れ替わる瞬間に過電流が流れる恐れがあるため，抵抗器\( \ \mathrm {R}_{2} \ \)で入力電流を制限します。

(b)解答：(2)
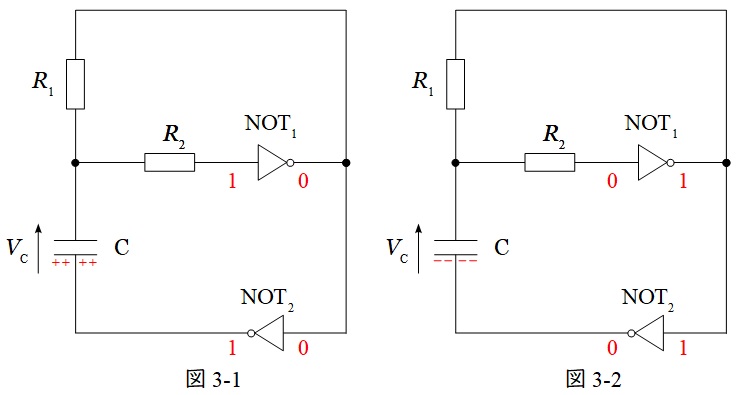
まず\( \ \mathrm {NOT}_{1} \ \)に\( \ 1 \ \)(\(5 \ \mathrm {V} \))が入力された時の回路を図3-1に示す。
\( \ \mathrm {NOT}_{1} \ \)に\( \ 1 \ \)が入力されると，\( \ 0 \ \)(\( \ 0 \ \mathrm {V} \))が出力される。したがって，\( \ \mathrm {NOT}_{2} \ \)の入力は\( \ 0 \ \)となり，\( \ \mathrm {NOT}_{2} \ \)の出力は\( \ 1 \ \)となる。したがって，コンデンサには正電荷が貯まっていき，徐々に\( \ V_{\mathrm {C}} \ \)の電圧が下がっていく。
同様に\( \ \mathrm {NOT}_{1} \ \)に\( \ 0 \ \)が入力された時の回路を図3-2に示す。
\( \ \mathrm {NOT}_{1} \ \)に\( \ 0 \ \)が入力されると，\( \ 1 \ \)が出力される。したがって，\( \ \mathrm {NOT}_{2} \ \)の入力は\( \ 1 \ \)となり，\( \ \mathrm {NOT}_{2} \ \)の出力は\( \ 0 \ \)となる。したがって，コンデンサには負電荷が貯まっていき，徐々に\( \ V_{\mathrm {C}} \ \)の電圧が上がっていく。
過渡現象を鑑み，この波形を表しているのは(2)となる。