【問題】
【難易度】★★☆☆☆(やや易しい)
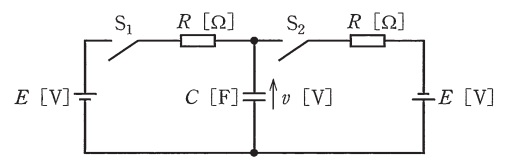
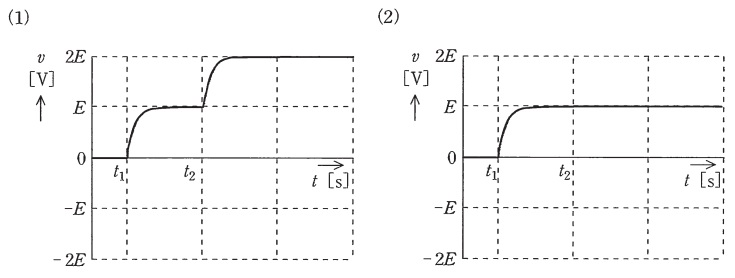
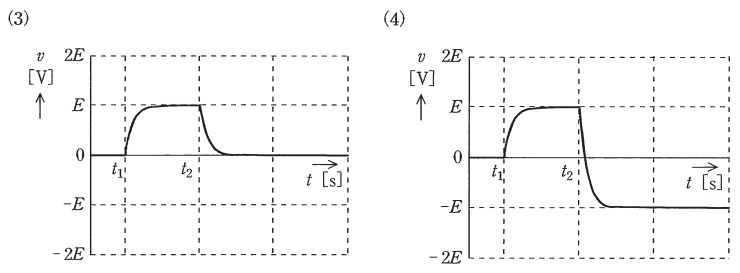
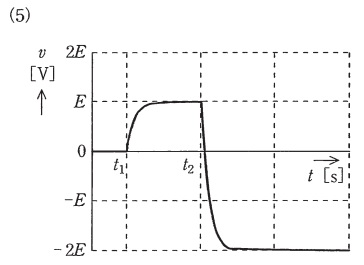
図のように,直流電圧\(E \ \mathrm {[V]}\)の電源が2個,\(R \ \mathrm {[\Omega ]}\)の抵抗が2個,静電容量\(C \ \mathrm {[F]}\)のコンデンサ,スイッチ\(S_{1}\)と\(S_{2}\)からなる回路がある。スイッチ\(S_{1}\)と\(S_{2}\)の初期状態は,共に開いているものとする。電源の内部インピーダンスは零とする。時刻\(t=t_{1} \ \mathrm {[s]}\)でスイッチ\(S_{1}\)を閉じ,その後,時定数\(CR \ \mathrm {[s]}\)に比べて十分に時間が経過した時刻\(t=t_{2} \ \mathrm {[s]}\)でスイッチ\(S_{1}\)を開き,スイッチ\(S_{2}\)を閉じる。このとき,コンデンサの端子電圧\(v \ \mathrm {[V]}\)の波形を示す図として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,コンデンサの初期電荷は零とする。
【ワンポイント解説】
過渡現象の内容を理解しているかを問う問題となっています。三種の場合は微分方程式の計算は必要ないので,解答を波形から暗記すると良いと思います。
1.\(RC\)直列回路の過渡現象
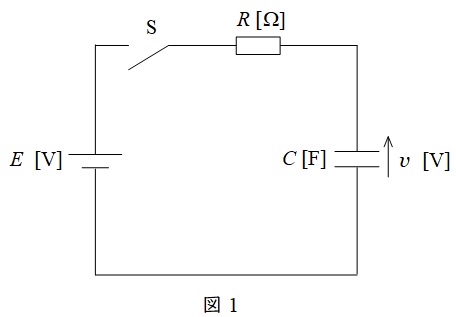
図1の\(RC\)直列回路において,スイッチ\(S\)を投入した時の過渡現象を考えます。
回路方程式は,
\[
\begin{eqnarray}
Ri +\frac {1}{C}\int i \mathrm {d}t &=&E \\[ 5pt ]
R\frac {\mathrm {d}q}{\mathrm {d}t} +\frac {q}{C} &=&E \\[ 5pt ]
\end{eqnarray}
\]
となる。定常解を\(q_{\mathrm {s}}\),過渡解を\(q_{\mathrm {t}}\)とすると,定常解は\(\displaystyle \frac {\mathrm {d}q}{\mathrm {d}t}\)であるから,
\[
\begin{eqnarray}
\frac {q_{\mathrm {s}}}{C} &=&E \\[ 5pt ]
q_{\mathrm {s}} &=&CE \\[ 5pt ]
\end{eqnarray}
\]
となる。過渡解は\(E=0\)とすると,
\[
\begin{eqnarray}
R\frac {\mathrm {d}q_{\mathrm {t}}}{\mathrm {d}t} +\frac {q_{\mathrm {t}}}{C} &=&0 \\[ 5pt ]
R\frac {\mathrm {d}q_{\mathrm {t}}}{\mathrm {d}t} &=&-\frac {q_{\mathrm {t}}}{C} \\[ 5pt ]
\frac {1}{q_{\mathrm {t}}}\mathrm {d}q_{\mathrm {t}} &=&-\frac {1}{RC}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
と整理できるので,両辺積分すると,
\[
\begin{eqnarray}
\ln q_{\mathrm {t}} &=&-\frac {1}{RC}t +C ( Cは積分定数 ) \\[ 5pt ]
q_{\mathrm {t}} &=&A\mathrm {e} ^{-\frac {1}{RC}t} ( A=\mathrm {e}^{C} ) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって,一般解は,
\[
\begin{eqnarray}
q &=&q_{\mathrm {s}}+q_{\mathrm {t}} \\[ 5pt ]
&=&CE+A\mathrm {e} ^{-\frac {1}{RC}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。ここで,初期状態での蓄えられる電荷は零であるから,
\[
\begin{eqnarray}
0&=&CE+A\mathrm {e} ^{-\frac {1}{RC}\times 0} \\[ 5pt ]
A&=&-CE \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
q &=&CE \left( 1-\mathrm {e} ^{-\frac {1}{RC}t}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。両辺微分すると,
\[
\begin{eqnarray}
i &=&\frac {E}{R} \mathrm {e} ^{-\frac {1}{RC}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,コンデンサの電圧\(v\)は,
\[
\begin{eqnarray}
v &=&\frac {q}{C} \\[ 5pt ]
&=&E \left( 1-\mathrm {e} ^{-\frac {1}{RC}t}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
【関連する「電気の神髄」記事】
【解答】
解答:(4)
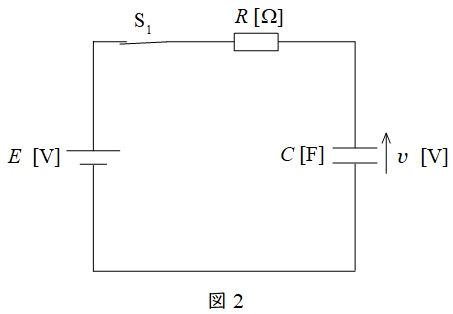
初期状態からスイッチ\(S_{1}\)を閉じると,回路は図2のようになり,ワンポイント解説「1.\(RC\)直列回路の過渡現象」の通り,コンデンサの電圧\(v\)は,
\[
\begin{eqnarray}
v &=&E \left( 1-\mathrm {e} ^{-\frac {1}{RC}t}\right) \\[ 5pt ]
\end{eqnarray}
\]
であるため,十分時間が経った状態\(t → \infty\)では,
\[
\begin{eqnarray}
v &=&E \\[ 5pt ]
\end{eqnarray}
\]
となる。
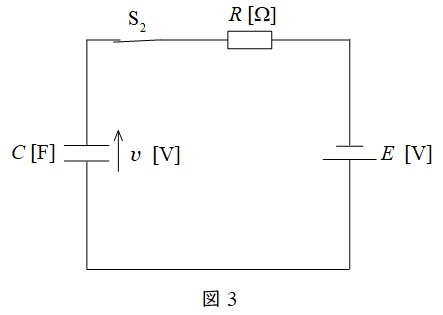
次にスイッチ\(S_{1}\)を開き,スイッチ\(S_{2}\)を閉じると図3のようになり,十分に時間が経った状態では,
\[
\begin{eqnarray}
v &=&-E \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,この条件を満たす選択肢は(4)となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは