《理論》〈電子理論〉[H28:問13]エミッタ接地トランジスタ増幅回路に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

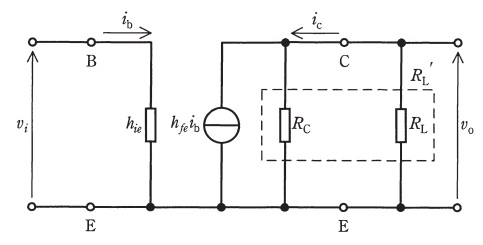
図は，エミッタ(\( \ \mathrm {E} \ \))を接地したトランジスタ増幅回路の簡易小信号等価回路である。この回路においてコレクタ抵抗\( \ R_{\mathrm {C}} \ \)と負荷抵抗\( \ R_{\mathrm {L}} \ \)の合成抵抗\( \ {R_{\mathrm {L}}}^{\prime }=\mathrm {1 \ k\Omega } \ \)のとき，電圧利得は\( \ \mathrm {40 \ dB} \ \)であった。入力電圧\( \ v_{\mathrm {i}}=10 \ \mathrm {mV} \ \)を加えたときにベース(\( \ \mathrm {B} \ \))に流れる入力電流\( \ i_{\mathrm {b}} \ \)の値\( \ [ \mathrm {\mu A} ] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし，\( \ v_{\mathrm {o}} \ \)は合成抵抗\( \ {R_{\mathrm {L}}}^{\prime } \ \)の両端における出力電圧，\( \ i_{\mathrm {C}} \ \)はコレクタ(\( \ \mathrm {C} \ \))に流れる出力電流，\( \ h_{\mathrm {ie}} \ \)はトランジスタの入力インピーダンスであり，小信号電流増幅率\( \ h_{\mathrm {fe}}=100 \ \)とする。

(1)　\( \ 0.1 \ \)　　(2)　\( \ 1 \ \)　　(3)　\( \ 10 \ \)　　(4)　\( \ 100 \ \)　　(5)　\( \ 1000 \ \)

【ワンポイント解説】

電圧利得の式を理解しているかどうかを問う問題で，公式を理解していればあとは単純な回路計算となります。

1.電圧増幅度\( \ A_{\mathrm {v}} \ \)と電圧利得\( \ G_{\mathrm {v}} \ \)
入力電圧が\( \ v_{\mathrm {i}} \ \)，出力電圧が\( \ v_{\mathrm {o}} \ \)の時，電圧増幅度\( \ A_{\mathrm {v}} \ \)と電圧利得\( \ G_{\mathrm {v}} \ \)は以下の式で求められます。
\[
\begin{eqnarray}
A_{\mathrm {v}}&=&\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}} \right| \\[ 5pt ] G_{\mathrm {v}}&=&20\log _{10} {A_{\mathrm {v}}} \\[ 5pt ] &=&20\log _{10} {\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}} \right|} \ \mathrm { [ \mathrm {dB} ] } \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(3)
問題図より，
\[
\begin{eqnarray}
v_{\mathrm {i}}&=&h_{\mathrm {ie}}i_{\mathrm {b}} \\[ 5pt ] v_{\mathrm {o}}&=&-R_{\mathrm {L}}^{\prime }i_{\mathrm {c}} \\[ 5pt ] &=&-{R_{\mathrm {L}}}^{\prime }h_{\mathrm {fe}}i_{\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\] であるから，電圧利得\( \ G_{\mathrm {v}} \ \)は
\[
\begin{eqnarray}
20\log _{10} {\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}} \right|} &=&40 \\[ 5pt ] 20\log _{10} {\left| \frac {-{R_{\mathrm {L}}}^{\prime }h_{\mathrm {fe}}i_{b}}{h_{\mathrm {ie}}i_{b}} \right|} &=&40 \\[ 5pt ] 20\log _{10} {\frac {{R_{\mathrm {L}}}^{\prime }h_{\mathrm {fe}}}{h_{\mathrm {ie}}}} &=&40 \\[ 5pt ] \log _{10} {\frac {{R_{\mathrm {L}}}^{\prime }h_{\mathrm {fe}}}{h_{\mathrm {ie}}}} &=&2 \\[ 5pt ] \frac {{R_{\mathrm {L}}}^{\prime }h_{\mathrm {fe}}}{h_{\mathrm {ie}}} &=&100
\end{eqnarray}
\] となる。\( \ {R_{\mathrm {L}}}^{\prime }=\mathrm {1k\Omega } \ \)，\( \ h_{\mathrm {fe}}=100 \ \)を代入すると，
\[
\begin{eqnarray}
\frac {1000 \times 100}{h_{\mathrm {ie}}} &=&100 \\[ 5pt ] h_{\mathrm {ie}}&=&1000 [ \Omega ] \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ i_{\mathrm {b}} \ \)は，
\[
\begin{eqnarray}
i_{\mathrm {b}}&=&\frac {v_{\mathrm {i}}}{h_{\mathrm {ie}}} \\[ 5pt ] &=&\frac {10\times 10 ^{-3}}{1000} \\[ 5pt ] &=&10\times 10^{-6} [ \mathrm{A} ] \\[ 5pt ] &=&10 \ [ \mathrm{\mu A} ] \\[ 5pt ] \end{eqnarray}
\] と求められる。