Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
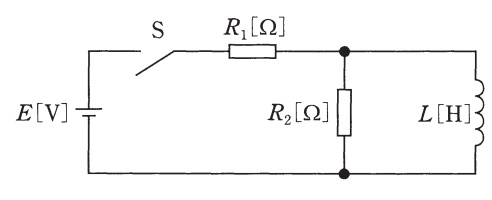
図のように,電圧\( \ E \ \left[ \mathrm {V} \right] \ \)の直流電源に,開いた状態のスイッチ\( \ \mathrm {S} \ \),\( \ R_{1} \ \left[ \Omega \right] \ \)の抵抗,\( \ R_{2} \ \left[ \Omega \right] \ \)の抵抗及び電流が\( \ 0 \ \mathrm {A} \ \)のコイル(インダクタンス\( \ L \ \left[ \mathrm {H}\right] \ \))を接続した回路がある。次の文章は,この回路に関する記述である。
1 スイッチ\( \ \mathrm {S} \ \)を閉じた瞬間(時刻\( \ t \ \mathrm {=0 \ \mathrm {s}} \ \))に\( \ R_{1} \ \left[ \Omega \right] \ \)の抵抗に流れる電流は\( \ \fbox { (ア) } \ \left[ \mathrm {A}\right] \ \)となる。
2 スイッチ\( \ \mathrm {S} \ \)を閉じて回路が定常状態とみなせるとき,\( \ R_{1} \ \left[ \Omega \right] \ \)の抵抗に流れる電流は,\( \ \fbox { (イ) } \ \left[ \mathrm {A}\right] \ \)となる。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& (ア) & (イ) \\
\hline
(1) & \displaystyle \frac {E}{R_{1}+R_{2}} & \displaystyle \frac {E}{R_{1}} \\
\hline
(2) & \displaystyle \frac {R_{2}E}{\left( R_{1}+R_{2}\right) R_{1}} & \displaystyle \frac {E}{R_{1}} \\
\hline
(3) & \displaystyle \frac {E}{R_{1}} & \displaystyle \frac {E}{R_{1}+R_{2}} \\
\hline
(4) & \displaystyle \frac {E}{R_{1}} & \displaystyle \frac {E}{R_{1}} \\
\hline
(5) & \displaystyle \frac {E}{R_{1}+R_{2}} & \displaystyle \frac {E}{R_{1}+R_{2}} \\
\hline
\end{array}
\]
【ワンポイント解説】
インダクタンスはスイッチを閉じた瞬間(過渡状態)は電流が流れず,十分時間が経つ(定常状態)と抵抗値がゼロになるという特性があります。この始動電流が小さいという特性を生かし,リアクトル始動をする機械もあります。
【解答】
解答:(1)
1 スイッチを閉じた瞬間
インダクタンスには電流が流れないので,インダクタンスは開放状態として考える。よって,電流はすべて\( \ R_{2} \ \)に流れるので,
\[
\begin{eqnarray}
I&=&\frac {E}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。
2 定常状態になった時
インダクタンスは抵抗値がゼロとなるので,電流はすべてインダクタンス側に流れるので,
\[
\begin{eqnarray}
I&=&\frac {E}{R_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは