《理論》〈電子理論〉[R4上:問13]演算増幅器を用いたシュミットトリガ回路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，図1の回路の動作について述べたものである。

図1は，演算増幅器(オペアンプ)を用いたシュミットトリガ回路である。この演算増幅器には\( \ +5 \ \mathrm {V} \ \)の単電源が供給されており，\( \ 0 \ \mathrm {V} \ \)から\( \ 5 \ \mathrm {V} \ \)までの範囲の電圧を出力できるものとする。

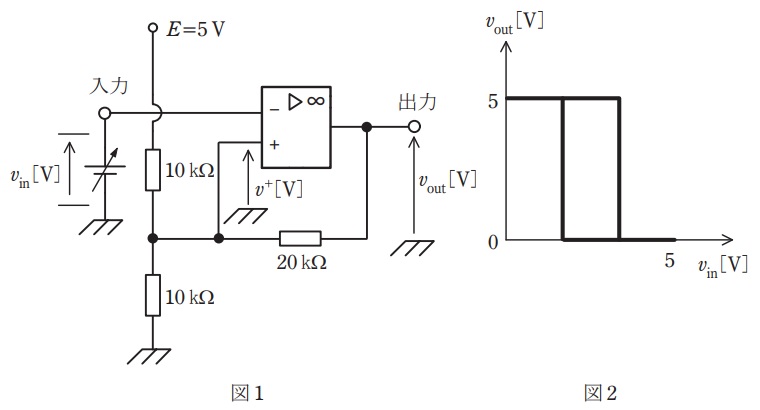
・出力電圧\( \ v_{\mathrm {out}} \ \)は\( \ 0～5 \ \mathrm {V} \ \)の間にあるため，演算増幅器の非反転入力の電圧\( \ v^{+} \ \mathrm {[V]} \ \)は\( \ \fbox {　 （ア） 　} \ \)の間にある。

・入力電圧\( \ v_{\mathrm {in}} \ \)を\( \ 0 \ \mathrm {V} \ \)から徐々に増加させると，\( \ v_{\mathrm {in}} \ \)が\( \ \fbox {　 （イ） 　} \ \mathrm {V} \ \)を上回った瞬間，\( \ v_{\mathrm {out}} \ \)は\( \ 5 \ \mathrm {V} \ \)から\( \ 0 \ \mathrm {V} \ \)に変化する。

・入力電圧\( \ v_{\mathrm {in}} \ \)を\( \ 5 \ \mathrm {V} \ \)から徐々に減少させると，\( \ v_{\mathrm {in}} \ \)が\( \ \fbox {　 （ウ） 　} \ \mathrm {V} \ \)を下回った瞬間，\( \ v_{\mathrm {out}} \ \)は\( \ 0 \ \mathrm {V} \ \)から\( \ 5 \ \mathrm {V} \ \)に変化する。

・入力\( \ v_{\mathrm {in}} \ \)に対する出力\( \ v_{\mathrm {out}} \ \)の変化を描くと，図2のような\( \ \fbox {　 （エ） 　} \ \)を示す特性となる。

上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　1.25～3.75　 & 　3.75　 & 　1.25　 & 　位相遅れ　 \\
\hline
(2) & 　1.25～3.75　 & 　1.25　 & 　3.75　 & 　ヒステリシス　 \\
\hline
(3) & 　2～3　 & 　2　 & 　3　 & 　ヒステリシス　 \\
\hline
(4) & 　2～3　 & 　2.75　 & 　2.25　 & 　位相遅れ　 \\
\hline
(5) & 　2～3　 & 　3　 & 　2　 & 　ヒステリシス　 \\
\hline
\end{array}
\]

【ワンポイント解説】

演算増幅器を用いたシュミットトリガ回路に関する問題です。
そもそもシュミットトリガとは入力に対して出力がヒステリシスに変化する回路のことなので，用語を知っていれば（エ）の空欄はそのまま入れるだけとなります。
回路図の書き換えを行い，電気回路の計算もする必要があるので，令和4年度上期の問題の中ではこの問題が最も難易度が高かったかと思います。

1.理想的な演算増幅器の特徴
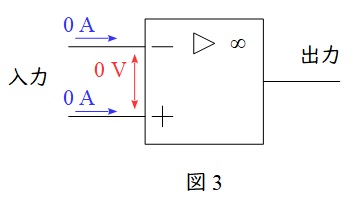
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)(バーチャルショート)となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

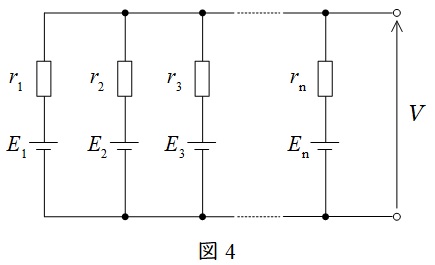
2.ミルマンの定理
図4のような，電源\( \ E_{1}，E_{2}，\cdots ，E_{\mathrm {n}} \ \)と抵抗\( \ r_{1}，r_{2}，\cdots ，r_{\mathrm {n}} \ \)が直並列された回路における全体の電圧\( \ V \ \)は，
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{r_{1}}+\frac {E_{2}}{r_{2}}+\frac {E_{3}}{r_{3}}+\cdots +\frac {E_{\mathrm {n}}}{r_{\mathrm {n}}}}{\displaystyle \frac {1}{r_{1}}+\frac {1}{r_{2}}+\frac {1}{r_{3}}+\cdots +\frac {1}{r_{\mathrm {n}}}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(5)
(ア)
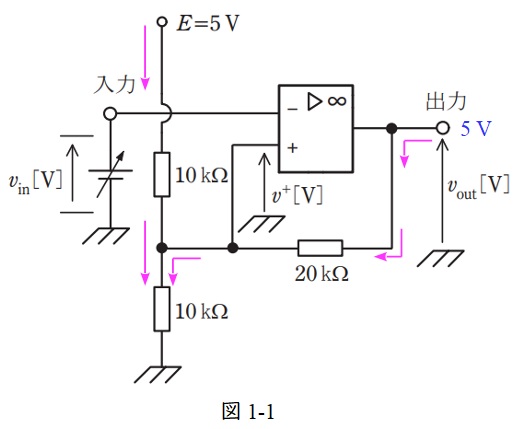
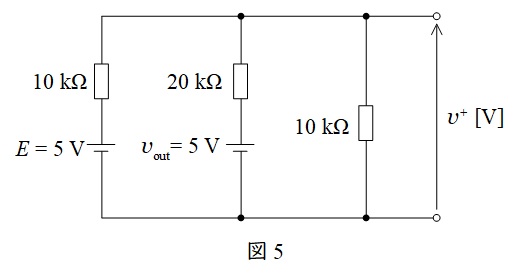
\( \ v_{\mathrm {out}} \ \)が\( \ 5 \ \mathrm {V} \ \)のとき，図1の回路での電流の流れは図1-1のようになる。したがって，そのときの回路は図5のように書き換えられる。
図5において\( \ v^{+} \ \mathrm {[V]} \ \)は，ワンポイント解説「2.ミルマンの定理」より，
\[
\begin{eqnarray}
v^{+}&=&\frac {\displaystyle \frac {E}{10\times 10^{3}}+\frac {v_{\mathrm {out}}}{20\times 10^{3}}+\frac {0}{10\times 10^{3}}}{\displaystyle \frac {1}{10\times 10^{3}}+\frac {1}{20\times 10^{3}}+\frac {1}{10\times 10^{3}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {5}{10\times 10^{3}}+\frac {5}{20\times 10^{3}}}{\displaystyle \frac {1}{10\times 10^{3}}+\frac {1}{20\times 10^{3}}+\frac {1}{10\times 10^{3}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {10+5}{20\times 10^{3}}}{\displaystyle \frac {2+1+2}{20\times 10^{3}}} \\[ 5pt ] &=&\frac {10+5}{2+1+2} \\[ 5pt ] &=&3 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

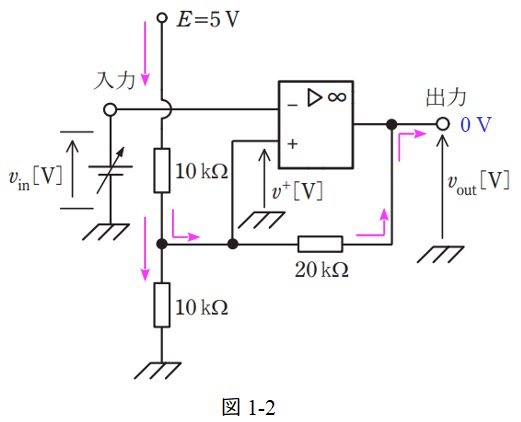
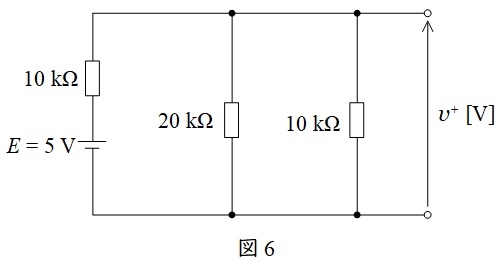
\( \ v_{\mathrm {out}} \ \)が\( \ 0 \ \mathrm {V} \ \)のとき，図1の回路での電流の流れは図1-2のようになる。したがって，そのときの回路は図6のように書き換えられる。
図6において\( \ v^{+} \ \mathrm {[V]} \ \)は，ワンポイント解説「2.ミルマンの定理」より，
\[
\begin{eqnarray}
v^{+}&=&\frac {\displaystyle \frac {E}{10\times 10^{3}}+\frac {v_{\mathrm {out}}}{20\times 10^{3}}+\frac {0}{10\times 10^{3}}}{\displaystyle \frac {1}{10\times 10^{3}}+\frac {1}{20\times 10^{3}}+\frac {1}{10\times 10^{3}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {5}{10\times 10^{3}}+\frac {0}{20\times 10^{3}}}{\displaystyle \frac {1}{10\times 10^{3}}+\frac {1}{20\times 10^{3}}+\frac {1}{10\times 10^{3}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {5}{10\times 10^{3}}}{\displaystyle \frac {2+1+2}{20\times 10^{3}}} \\[ 5pt ] &=&\frac {5\times 2}{2+1+2} \\[ 5pt ] &=&2 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，\( \ v^{+} \ \mathrm {[V]} \ \)は\( \ 2～3 \ \mathrm {V} \ \)の間となる。

※重ね合わせの理や分圧・分流の法則を用いても解答は導出可能です。

(イ)
（ア）より，\( \ v_{\mathrm {out}}=5 \ \mathrm {[V]} \ \)のとき，\( \ v^{+}=3 \ \mathrm {[V]} \ \)，\( \ v_{\mathrm {out}}=0 \ \mathrm {[V]} \ \)のとき，\( \ v^{+}=2 \ \mathrm {[V]} \ \)であるため，\( \ v_{\mathrm {out}}=5 \ \mathrm {[V]} \ \)\( \ \left( v^{+}=3 \ \mathrm {[V]}\right) \ \)の状態で\( \ v_{\mathrm {in}} \ \)を\( \ 0 \ \mathrm {V} \ \)から徐々に増加させると\( \ v_{\mathrm {in}}=3 \ \mathrm {[V]} \ \)を上回った瞬間に\( \ v_{\mathrm {in}}＞v^{+} \ \)となるため出力が反転する。

(ウ)
（イ）と同様に，\( \ v_{\mathrm {out}}=0 \ \mathrm {[V]} \ \)\( \ \left( v^{+}=2 \ \mathrm {[V]}\right) \ \)の状態で\( \ v_{\mathrm {in}} \ \)を\( \ 5 \ \mathrm {V} \ \)から徐々に減少させると\( \ v_{\mathrm {in}}=2 \ \mathrm {[V]} \ \)を下回った瞬間に\( \ v_{\mathrm {in}}＜v^{+} \ \)となるため出力が反転する。

(エ)
図2のような特性をヒステリシス特性といいます。