《理論》〈電気回路〉[R4下:問5]直流回路の端子電圧からの電源電圧の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

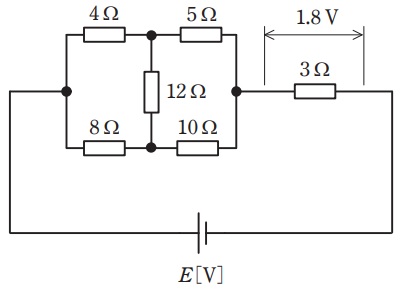
図のような直流回路において，抵抗\( \ 3 \ \mathrm {\Omega } \ \)の端子間の電圧が\( \ 1.8 \ \mathrm {V} \ \)であった。このとき，電源電圧\( \ E \ \mathrm {[V]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1.8 \ \)　　(2)　\( \ 3.6 \ \)　　(3)　\( \ 5.4 \ \)　　(4)　\( \ 7.2 \ \)　　(5)　\( \ 10.4 \ \)　　

【ワンポイント解説】

直流回路の端子電圧の値から電源電圧の値を導出する問題です。
回路が若干複雑に見えますが，抵抗値の関係に気付けば比較的時間をかけずに解けるかと思います。

1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.分圧・分流の法則
①分圧の法則
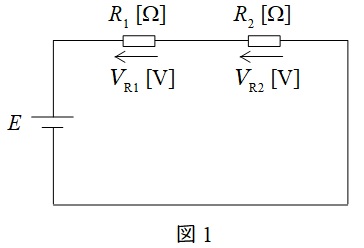
図1に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

②分流の法則
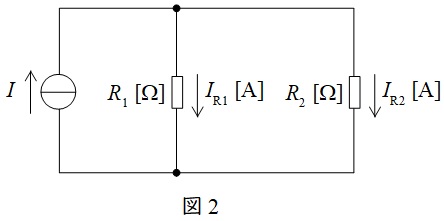
図2に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

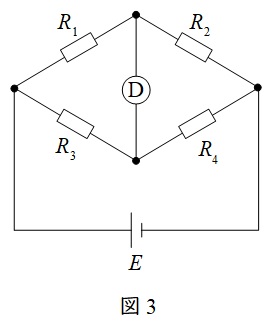
3.直流ブリッジの平衡条件
直流ブリッジ回路は抵抗の抵抗値を求める方法であり，ホイートストンブリッジと呼ばれます。
図3の回路において，検出器\( \ Ⓓ \ \)に電流が流れない条件を平衡条件と言い，
\[
\begin{eqnarray}
R_{1}R_{4} &=& R_{2}R_{3} \\[ 5pt ] \end{eqnarray}
\] の関係があります。したがって，３つの既知の抵抗があれば，残りの１つの抵抗値を求めることができます。

【解答】

解答：(3)
ワンポイント解説「3.直流ブリッジの平衡条件」の通り，問題図のブリッジ回路は平衡条件を満たしているので\( \ 12 \ \mathrm {\Omega } \ \)の抵抗には電流が流れず無視できる。
このとき\( \ 4 \ \mathrm {\Omega } \ \)，\( \ 5 \ \mathrm {\Omega } \ \)，\( \ 8 \ \mathrm {\Omega } \ \)，\( \ 10 \ \mathrm {\Omega } \ \)の抵抗の合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「1.合成抵抗」の通り，
\[
\begin{eqnarray}
R&=&\frac {\left( 4+5\right) \times \left( 8+10\right) }{\left( 4+5\right) +\left( 8+10\right) } \\[ 5pt ] &=&\frac {9\times 18 }{9+18} \\[ 5pt ] &=&6 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，ワンポイント解説「2.分圧・分流の法則」を利用して電源電圧\( \ E \ \mathrm {[V]} \ \)を求めると，
\[
\begin{eqnarray}
1.8&=&\frac {3}{R+3}E \\[ 5pt ] &=&\frac {3}{6+3}E \\[ 5pt ] &=&\frac {1}{3}E \\[ 5pt ] E&=&5.4 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。