《理論》〈電磁気〉[R06上:問2]空気中の導体球に帯電できる電荷量に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

空気中に孤立した半径$\ a \ \mathrm {[m]} \ $の導体球に帯電できる最大の電荷の値$\ \mathrm {[C]} \ $として，正しいものを次の(1)～(5)のうちから一つ選べ。ただし，空気の絶縁耐力及び誘電率はそれぞれ$\ E_{\mathrm {m}} \ \mathrm {[V / m]} \ $及び$\ \varepsilon_{0} \ \mathrm {[F/m]} \ $とする。

　(1)　$\ \displaystyle \frac {E_{\mathrm {m}}}{4\pi \varepsilon _{0}a^{2}} \ $　　(2)　$\ \displaystyle \frac {E_{\mathrm {m}}}{4\pi \varepsilon _{0}a} \ $　　(3)　$\ 4\pi \varepsilon _{0}aE_{\mathrm {m}} \ $　
　(4)　$\ 4\pi \varepsilon _{0}a^{2}E_{\mathrm {m}} \ $　　(5)　$\ 4\pi \varepsilon _{0}a^{3}E_{\mathrm {m}} \ $

【ワンポイント解説】

空気中においた導体球に帯電可能な電荷量を求める問題です。
まずは，最大の電荷を帯電したと仮定し解いていくことがコツとなります。合格のためにはぜひとも解いておきたい問題です。
本問は平成11年問5からの再出題となります。

1.真空中の電界の大きさ
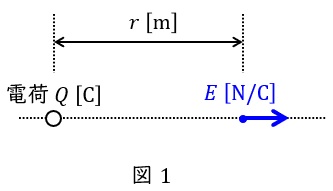
真空中に電荷$\ Q \ \mathrm {[C]} \ $をおいた時，電荷から距離$\ r \ \mathrm {[m]} \ $離れた場所の電界の大きさ$\ E \ \mathrm {[N / C]} \ $は，真空の誘電率を$\ \varepsilon _{0} \ \mathrm {[F / m]} \ $とすると，

$$\begin{eqnarray} E &=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}$$ となります。

【解答】

解答：(4)
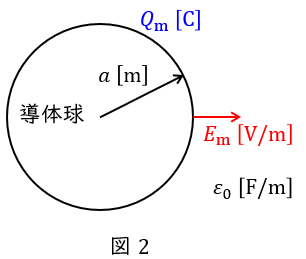
図2に示すように，導体球に空気の絶縁耐力を超えない最大の電荷$\ Q_{\mathrm {m}} \ \mathrm {[C]} \ $を加えたとすると，このときの導体表面の電界は$\ E_{\mathrm {m}} \ \mathrm {[V / m]} \ $となるので，ワンポイント解説「1.真空中の電界の大きさ」の通り，

$$\begin{eqnarray} E_{\mathrm {m}} &=&\frac {Q_{\mathrm {m}}}{4\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}$$ となる。これを$\ Q_{\mathrm {m}} \ $について整理すれば，
$$\begin{eqnarray} Q_{\mathrm {m}} &=&4\pi \varepsilon _{0}a^{2}E_{\mathrm {m}} \\[ 5pt ] \end{eqnarray}$$ と求められる。