《理論》〈電気回路〉[R06下:問5]抵抗，コイル，コンデンサに蓄えられるエネルギーに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

\( \ R_{1} ＝ 20 \ \Omega \ \)，\( \ R_{2} ＝ 30 \ \Omega \ \)の抵抗，インダクタンス\( \ L_{1} ＝ 20 \ \mathrm {mH} \ \)，\( \ L_{2} ＝ 40 \ \mathrm {mH} \ \)のコイル及び静電容量\( \ C_{1} ＝ 400 \ \mathrm {\mu F} \ \)，\( \ C_{2} ＝ 600 \ \mathrm {\mu F} \ \)のコンデンサからなる図のような直並列回路がある。直流電圧\( \ E ＝100 \ \mathrm {V} \ \)を加えたとき，定常状態において\( \ L_{1} \ \)，\( \ L_{2} \ \)，\( \ C_{1} \ \)及び\( \ C_{2} \ \)に蓄えられるエネルギーの総和の値\( \ \mathrm {[J]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

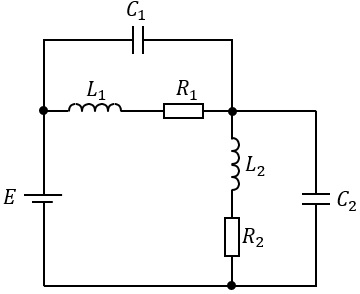
　(1)　\( \ 0.12 \ \)　　(2)　\( \ 1.20 \ \)　　(3)　\( \ 1.32 \ \)　　(4)　\( \ 1.40 \ \)　　(5)　\( \ 1.52 \ \)

【ワンポイント解説】

抵抗，コイル，コンデンサを直並列した回路の定常状態において蓄えられるエネルギーの総和を求める問題です。
まずは定常状態における回路の状態を考えることが重要です。それぞれの素子の特性を理解して解くようにして下さい。
本問は平成29年問6からの再出題となります。

1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

2.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので，電流がものすごく流れやすい状態，すなわち短絡として考えます。

② 定常状態
コンデンサに十分に電荷が蓄えられているので，電流をこれ以上蓄えようとしない，すなわち開放として考えます。

3.自己インダクタンス\( \ L \ \)と蓄積される電磁エネルギー\( \ W \ \)の関係式
自己インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルに電流\( \ I \ \mathrm {[A]} \ \)を流し，十分時間が経過した時にコイルに蓄えられるエネルギー\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W&=&\frac {1}{2}LI^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

4.コンデンサの静電エネルギー\( \ W \ \)
コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)に電圧\( \ V \ \mathrm {[V]} \ \)が加わっているとすると，十分時間が経過した時にコンデンサに蓄えられる静電エネルギー\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ Q=CV \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
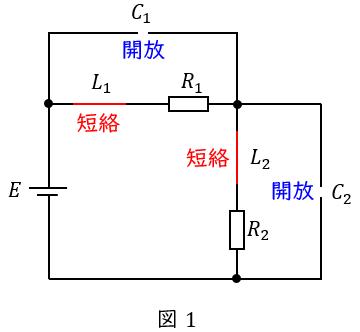
ワンポイント解説「1.過渡現象におけるリアクトルの過渡状態と定常状態」及び「2.過渡現象におけるコンデンサの過渡状態と定常状態」の通り，定常状態においてはコイルは短絡，コンデンサは開放と考えれば良いので，回路は図1のようになる。
したがって，\( \ L_{1} \ \)及び\( \ L_{2} \ \)に流れる電流\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I &=&\frac {E}{R_{1}+R_{2}} \\[ 5pt ] &=&\frac {100}{20+30} \\[ 5pt ] &=&2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ C_{1} \ \)及び\( \ C_{2} \ \)に加わる電圧\( \ V_{1} \ \mathrm {[V]} \ \)及び\( \ V_{2} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{1} &=&R_{1}I \\[ 5pt ] &=&20\times 2 \\[ 5pt ] &=&40 \ \mathrm {[V]} \\[ 5pt ] V_{2} &=&R_{2}I \\[ 5pt ] &=&30\times 2 \\[ 5pt ] &=&60 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，\( \ L_{1} \ \)，\( \ L_{2} \ \)，\( \ C_{1} \ \)及び\( \ C_{2} \ \)に蓄えられるエネルギーの総和\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}L_{1}I^{2}+\frac {1}{2}L_{2}I^{2}+\frac {1}{2}C_{1}V_{1}^{2}+\frac {1}{2}C_{2}V_{2}^{2} \\[ 5pt ] &=&\frac {1}{2}\times 20\times 10^{-3}\times 2^{2}+\frac {1}{2}\times 40\times 10^{-3}\times 2^{2}+\frac {1}{2}\times 400\times 10^{-6}\times 40^{2}+\frac {1}{2}\times 600\times 10^{-6}\times 60^{2} \\[ 5pt ] &=&0.04+0.08+0.32+1.08 \\[ 5pt ] &=&1.52 \ \mathrm {[J]} \\[ 5pt ] \end{eqnarray}
\] と求められる。