《理論》〈電子理論〉[R07上:問12]電極から放出される電子の運動に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

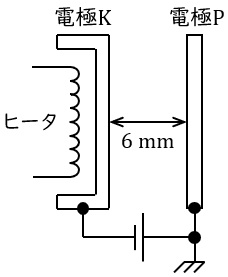
真空中において，図のように電極板の間隔が\( \ 6 \ \mathrm {mm} \ \)，電極板の面積が十分広い平行平板電極があり，電極\( \ \mathrm {K} \ \)，\( \ \mathrm {P} \ \)間には\( \ 2 \ 000 \ \mathrm {V} \ \)の直流電圧が加えられている。このとき，電極\( \ \mathrm {K} \ \)，\( \ \mathrm {P} \ \)間の電界の強さは約\( \ \fbox {　 （ア） 　} \ \mathrm {V / m} \ \)である。電極\( \ \mathrm {K} \ \)をヒータで加熱すると表面から\( \ \fbox {　 （イ） 　} \ \)が放出される。ある\( \ 1 \ \)個の電子に着目してその初速度を零とすれば，電子が電極\( \ \mathrm {P} \ \)に達したときの運動エネルギー\( \ W \ \)は\( \ \fbox {　 （ウ） 　} \ \mathrm {J} \ \)となる。

ただし，電極\( \ \mathrm {K} \ \)，\( \ \mathrm {P} \ \)間の電界は一様とし，電気素量 \( \ e=1.6\times 10^{-19} \ \mathrm {C} \ \)とする。

上記の記述中の空白箇所(ア)～(ウ)に当てはまる語句又は数値の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　3.3\times 10^{2}　 & 　光電子　 & 　1.6\times 10^{-16}　 \\
\hline
(2) & 　3.3\times 10^{5}　 & 　熱電子　 & 　1.6\times 10^{-16}　 \\
\hline
(3) & 　3.3\times 10^{2}　 & 　光電子　 & 　3.2\times 10^{-16}　 \\
\hline
(4) & 　3.3\times 10^{2}　 & 　熱電子　 & 　1.6\times 10^{-16}　 \\
\hline
(5) & 　3.3\times 10^{5}　 & 　熱電子　 & 　3.2\times 10^{-16}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

ヒータにより電極から放出される電子の運動に関する問題で，電磁気の公式を応用して解く問題となります。
本問では電極\( \ \mathrm {P} \ \)に到達したときの電子の速度を求める内容は出題されていませんが，求められるようにしておくことをお勧めします。
本問は平成18年問12の再出題となります。

1.熱電子放出
金属または半導体等の固体を高温に熱したとき，自由電子の運動が激しくなり固体表面のエネルギー障壁を超え飛び出すことを言います。このとき飛び出した電子を熱電子といいます。

2.光電子放出
金属等にエネルギーの強い紫外光等を照射すると，光のエネルギーが電子に与えられ，電子が放出する現象をいい，光電効果ともいいます。このとき飛び出した電子を光電子といいます。

3.電界中の電子の運動
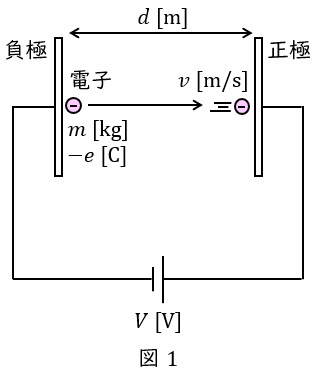
図1のように，極板間距離\( \ d \ \mathrm {[m]} \ \)の電極間に電圧\( \ V \ \mathrm {[V]} \ \)を加えたときの電子の運動を考えます。
まず，負極側にある電子について考えます。最初，電子の速度が零であるとすると，電子が受ける力\( \ F \ \mathrm {[N]} \ \)は電界の大きさに比例し，極板内の電界が\( \ \displaystyle E=\frac {V}{d} \ \mathrm {[V/m]} \ \)であることから，
\[
\begin{eqnarray}
F&=&eE \\[ 5pt ] &=&\frac {eV}{d} \\[ 5pt ] \end{eqnarray}
\] となります。物体の運動方程式より，電子の質量\( \ m \ \mathrm {[kg]} \ \)，加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)とすると，\( \ F=ma \ \)の関係があるので，
\[
\begin{eqnarray}
a&=&\frac {F}{m} \\[ 5pt ] &=&\frac {eV}{md} \\[ 5pt ] \end{eqnarray}
\] で加速されます。したがって，電子の加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)は電圧\( \ V \ \mathrm {[V]} \ \)に比例することが分かります。

次に，電子が距離\( \ d \ \mathrm {[m]} \ \)動き，反対側の電極に到達したときの電子の速度\( \ v \ \mathrm {[m/s]} \ \)を考えます。負極での電子の位置エネルギーは\( \ W=eV \ \mathrm {[J]} \ \)であり，電子が正極に到達したときの運動エネルギーが\( \ \displaystyle W=\frac {1}{2}mv^{2} \ \mathrm {[J]} \ \)なので，エネルギー保存の法則により位置エネルギーがすべて運動エネルギーになったとすると，
\[
\begin{eqnarray}
eV&=&\frac {1}{2}mv^{2} \\[ 5pt ] v^{2}&=&\frac {2eV}{m} \\[ 5pt ] v&=&\sqrt {\frac {2eV}{m}} \\[ 5pt ] \end{eqnarray}
\] になります。

【解答】

解答：(5)
(ア)
直流電圧\( \ V=2 \ 000 \ \mathrm {[V]} \ \)，電極板の間隔\( \ d=6 \ \mathrm {[mm]} \ \)なので，\( \ \mathrm {K} \ \)，\( \ \mathrm {P} \ \)間の電界の強さ\( \ E \ \mathrm {[V / m]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ] &=&\frac {2 \ 000}{6\times 10^{-3}} \\[ 5pt ] &≒&3.3\times 10^{5} \ \mathrm {[V / m]} \\[ 5pt ] \end{eqnarray}
\] となります。

(イ)
ワンポイント解説「1.熱電子放出」の通り，電極をヒータで加熱すると表面から放出される電子を熱電子をいいます。

(ウ)
ワンポイント解説「3.電界中の電子の運動」の通り，電子が電極\( \ \mathrm {P} \ \)に達したときの運動エネルギー\( \ W \ \mathrm {[J]} \ \)は，電極\( \ \mathrm {K} \ \)における位置エネルギーと等しいので，
\[
\begin{eqnarray}
W&=&eV \\[ 5pt ] &=&1.6\times 10^{-19}\times 2 \ 000 \\[ 5pt ] &=&3.2\times 10^{-16} \ \mathrm {[J]} \\[ 5pt ] \end{eqnarray}
\] となります。