【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,\( \ RLC \ \)直列共振回路に関する記述である。
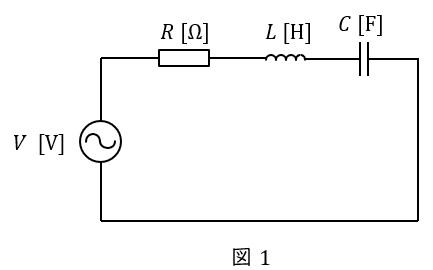
\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗,インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイル,静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサを直列に接続した回路がある。
この回路に交流電圧を加え,その周波数を変化させると,特定の周波数\( \ f_{\mathrm {r}} \ \mathrm {[Hz]} \ \)のときに誘導性リアクタンス\( \ =2\pi f_{\mathrm {r}}L \ \mathrm {[\Omega ]} \ \)と容量性リアクタンス\( \ \displaystyle =\frac {1}{2\pi f_{\mathrm {r}}C} \ \mathrm {[\Omega ]} \ \)の大きさが等しくなり,その作用が互いに打ち消し合って回路のインピーダンスが\( \ \fbox { (ア) } \ \)なり,\( \ \fbox { (イ) } \ \)電流が流れるようになる。この現象を直列共振といい,このときの周波数\( \ f_{\mathrm {r}} \ \mathrm {[Hz]} \ \)をその回路の共振周波数という。回路のリアクタンスは共振周波数\( \ f_{\mathrm {r}} \ \mathrm {[Hz]} \ \)より低い周波数では\( \ \fbox { (ウ) } \ \)となり,電圧より位相が\( \ \fbox { (エ) } \ \)電流が流れる。また,共振周波数\( \ f_{\mathrm {r}} \ \mathrm {[Hz]} \ \)より高い周波数では\( \ \fbox { (オ) } \ \)となり,電圧より位相が\( \ \fbox { (カ) } \ \)電流が流れる。
上記の記述中の空白箇所(ア)~(カ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccccc}
& (ア) & (イ) & (ウ) & (エ) & (オ) & (カ) \\
\hline
(1) & 大きく & 小さな & 容量性 & 進んだ & 誘導性 & 遅れた \\
\hline
(2) & 小さく & 大きな & 誘導性 & 遅れた & 容量性 & 進んだ \\
\hline
(3) & 小さく & 大きな & 容量性 & 進んだ & 誘導性 & 遅れた \\
\hline
(4) & 大きく & 小さな & 誘導性 & 遅れた & 容量性 & 進んだ \\
\hline
(5) & 小さく & 大きな & 容量性 & 遅れた & 誘導性 & 進んだ \\
\hline
\end{array}
\]
【ワンポイント解説】
直列共振に関する問題です。
直列共振と並列共振は共振周波数の導出式は全く同じ式となりますが,途中の過程やその特性は全く異なります。
電験ではその辺りの理解も問われますので,必ず理解しておくようにしましょう。
平成24年問7に同じ問題が出題されています。
1.直列回路の共振回路
図1のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \)は,角周波数を\( \ \omega \ \)とすると,
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ]
&=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,インピーダンスが最も小さくなるためには,上式の虚数部が零である必要があります。よって,共振角周波数\( \ \omega _{\mathrm {c}} \ \)は,
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ]
\omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ]
\omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ]
\omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,共振周波数を\( \ f_{\mathrm {c}} \ \)とすると,\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より,
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
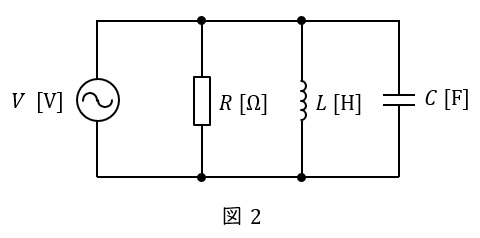
2.並列回路の共振回路
図2のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \)は,角周波数を\( \ \omega \ \)とすると,
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ]
&=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\]
となり,アドミタンスが最も小さくなるためには,上式の虚数部が零である必要があります。よって,共振角周波数\( \ \omega _{\mathrm {c}} \ \)は,
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ]
\omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ]
\omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ]
\omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,共振周波数を\( \ f_{\mathrm {c}} \ \)とすると,\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より,
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
解答:(3)
(ア)
ワンポイント解説「1.直列回路の共振回路」の通り,直列共振状態においては回路のインピーダンスは小さくなります。
(イ)
回路のインピーダンスは小さくなると,当然大きな電流が流れるようになります。その値は図1において,
\[
\begin{eqnarray}
I&=&\frac {V}{R} \\[ 5pt ]
\end{eqnarray}
\]
となります。
(ウ)
(エ)
ワンポイント解説「1.直列回路の共振回路」より,回路のインピーダンスは,
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\left( 2\pi f L -\frac {1}{2\pi f C}\right)
\end{eqnarray}
\]
で与えられ,共振周波数より低ければ\( \ \displaystyle \frac {1}{2\pi f C} > 2\pi f L \ \)となり,この場合は電流の位相が電圧より進む容量性となります。
(オ)
(カ)
(ウ),(エ)と同様に,共振周波数より高ければ\( \ \displaystyle 2\pi f L > \frac {1}{2\pi f C} \ \)となり,この場合は電流の位相が電圧より遅れる誘導性となります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは