《法規》〈電気施設管理〉[H29:問13]水力発電所の発電電力量に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

自家用水力発電所をもつ工場があり，電力系統と常時系統連系している。
ここでは，自家用水力発電所の発電電力は工場内にて消費させ，同電力が工場の消費電力よりも大きくなり余剰が発生した場合，その余剰分は電力系統に逆潮流(送電)させる運用をしている。
この工場のある日(\(0\)時～\(24\)時)の消費電力と自家用水力発電所の発電電力はそれぞれ図1及び図2のように推移した。次の(a)及び(b)の問に答えよ。
なお，自家用水力発電所の所内電力は無視できるものとする。

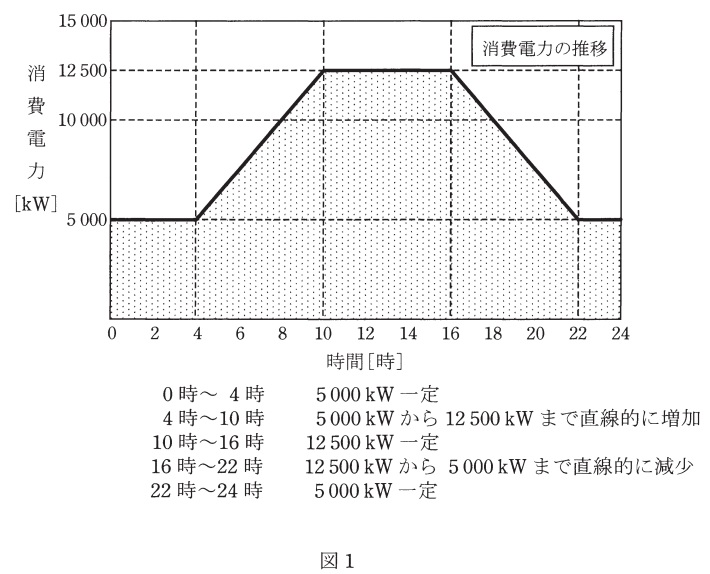
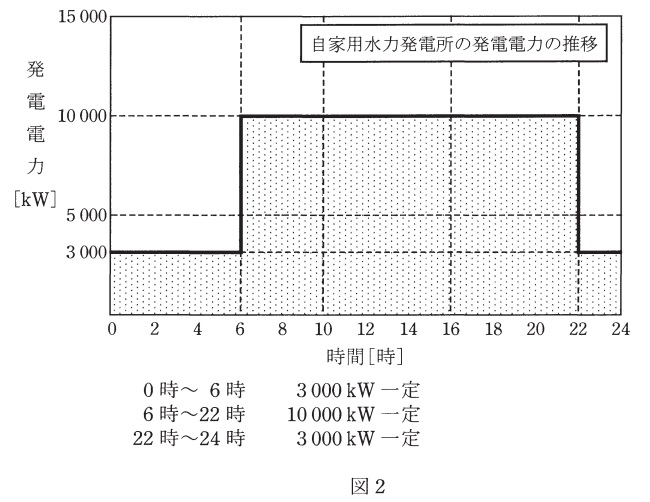
(a)　この日の電力系統への送電電力量の値\( \ [\mathrm {MW\cdot h}] \ \)と電力系統からの受電電力量の値\( \ [\mathrm {MW\cdot h}] \ \)の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& 送電電力量 \ \mathrm {[MW\cdot h]} & 受電電力量 \ \mathrm {[MW\cdot h]} \\
\hline
(1) & 12.5 & 26.0 \\
\hline
(2) & 12.5 & 38.5 \\
\hline
(3) & 26.0 & 38.5 \\
\hline
(4) & 38.5 & 26.0 \\
\hline
(5) & 26.0 & 12.5 \\
\hline
\end{array}
\]

(b)　この日，自家用水力発電所で発電した電力量のうち，工場内で消費された電力量の比率\( \ [％] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 18.3 \ \)　　(2)　\( \ 32.5 \ \)　　(3)　\( \ 81.7 \ \)　　(4)　\( \ 87.6 \ \)　　(5)　\( \ 93.2 \ \)

【ワンポイント解説】

まず図3のように，図1に図2の線を書き込み，イメージをつかみましょう。送電電力量と受電電力量どちらがどれぐらい多いかわかるので，選択肢を絞れ，計算ミスも防げます。

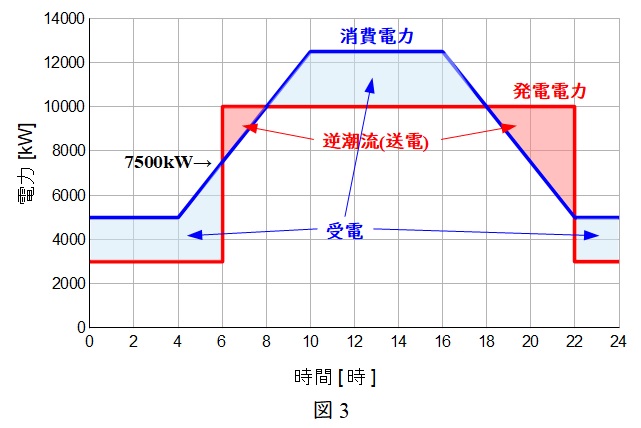
【解答】

(a)解答：(2)
送電電力量は図3の赤塗した箇所の面積である。\( \ 6 \ \)時から\( \ 8 \ \)時までの送電電力量\( \ W_{\mathrm {S1}} \ \)，\( \ 18 \ \)時から\( \ 22 \ \)時までの送電電力量\( \ W_{\mathrm {S2}} \ \)とすると，
\[
\begin{eqnarray}
W_{\mathrm {S1}}&=& ( 10 \ 000 – 7 \ 500 ) \times 2 ÷ 2 \\[ 5pt ] &=&2 \ 500 \ \mathrm {[kW\cdot h]} \\[ 5pt ] W_{\mathrm {S2}}&=& ( 10 \ 000 – 5 \ 000 ) \times 4 ÷ 2 \\[ 5pt ] &=&10 \ 000 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，送電電力量\( \ W_{\mathrm {S}} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {S}} &=& W_{\mathrm {S1}}+W_{\mathrm {S2}} \\[ 5pt ] &=& 2 \ 500+10 \ 000 \\[ 5pt ] &=& 12 \ 500 \ \mathrm {[kW\cdot h]} \\[ 5pt ] &=& 12.5 \ \mathrm {[MW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

受電電力量は図3の青塗した箇所の面積である。\( \ 0 \ \)時から\( \ 6 \ \)時までの受電電力量\( \ W_{\mathrm {R1}} \ \)，\( \ 8 \ \)時から\( \ 18 \ \)時までの受電電力量\( \ W_{\mathrm {R2}} \ \)，\( \ 22 \ \)時から\( \ 24 \ \)時までの受電電力量\( \ W_{\mathrm {R3}} \ \)とすると，
\[
\begin{eqnarray}
W_{\mathrm {R1}} &=& \left( 5 \ 000 – 3 \ 000 \right) \times 6 + \left( 7 \ 500 – 5 \ 000 \right) \times 2 ÷ 2 \\[ 5pt ] &=& 14 \ 500 \ \mathrm {[kW\cdot h]} \\[ 5pt ] W_{\mathrm {R2}} &=& \left( 6+10 \right) \times \left( 12 \ 500 – 10 \ 000 \right) ÷ 2 \\[ 5pt ] &=& 20000 \ \mathrm {[kW\cdot h]} \\[ 5pt ] W_{\mathrm {R3}} &=& \left( 5 \ 000 – 3 \ 000 \right) \times 2 \\[ 5pt ] &=& 4 \ 000 \ \mathrm {[kW\cdot h]}
\end{eqnarray}
\] となる。よって，受電電力量\( \ W_{\mathrm {R}} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {R}} &=& W_{\mathrm {R1}} + W_{\mathrm {R2}} + W_{\mathrm {R3}} \\[ 5pt ] &=& 14500 + 20000 + 4000 \\[ 5pt ] &=& 38500 \ [\mathrm {kW\cdot h}] \\[ 5pt ] &=& 38.5 \ [\mathrm {MW\cdot h}] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(5)
自家用水力発電所で発電した電力量\( \ W_{\mathrm {G}} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {G}} &=& 3000\times 6+10000\times 16+3000\times 2 \\[ 5pt ] &=& 184000 \ [\mathrm {kW\cdot h}] \\[ 5pt ] &=& 184 \ [\mathrm {MW\cdot h}] \end{eqnarray}
\] となる。工場内で消費された電力量\( \ W_{\mathrm {I}} \ \)は\( \ W_{\mathrm {I}}=W_{\mathrm {G}}-W_{\mathrm {S}}=184-12.5=171.5 \ [\mathrm {MW\cdot h}] \ \)であるから，その割合は，
\[
\begin{eqnarray}
\frac {W_{\mathrm {I}}}{W_{\mathrm {G}}}\times 100 &=& \frac {171.5}{184}\times 100 \\[ 5pt ] &≒& 93.2[％] \end{eqnarray}
\] と求められる。