Contents
【問題】
【難易度】★★★☆☆(普通)
図のように,三つの抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \),\( \ R_{2} \ \mathrm {[\Omega ]} \ \),\( \ R_{3} \ \mathrm {[\Omega ]} \ \)とインダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルと静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサが接続されている回路に\( \ V \ \mathrm {[V]} \ \)の直流電源が接続されている。定常状態において直流電源を流れる電流の大きさを表す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
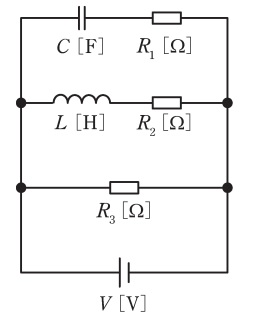
(1) \(\displaystyle \frac {V}{R_{3}}\) (2) \(\displaystyle \frac {V}{\displaystyle \frac {1}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{2}}}}\) (3) \(\displaystyle \frac {V}{\displaystyle \frac {1}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{3}}}}\)
(4) \(\displaystyle \frac {V}{\displaystyle \frac {1}{\displaystyle \frac {1}{R_{2}}+\frac {1}{R_{3}}}}\) (5) \(\displaystyle \frac {V}{\displaystyle \frac {1}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {1}{R_{3}}}}\)
【ワンポイント解説】
過渡現象に関してきちんと理解しているかを問う問題となっています。よく交流回路の特性と混同している方がいらっしゃいます。全く別物と理解して下さい。直流回路の過渡現象においてはリアクトルとコンデンサは逆の特性を示します。
1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって,リアクトルに電圧を印加した瞬間はほとんど電流は流れないので,開放として考えます。
② 定常状態
電圧を印加して十分時間が経過した後は,リアクトルの抵抗はほぼ零になります。したがって,短絡として考えます。
2.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので,電流がものすごく流れやすい状態,すなわち短絡として考えます。
② 定常状態
コンデンサに十分に電荷が蓄えられているので,電流をこれ以上蓄えようとしない,すなわち開放として考えます。
【解答】
解答:(4)
ワンポイント解説「1.過渡現象におけるリアクトルの過渡状態と定常状態」の通り,定常状態においてはリアクトルは短絡,また,ワンポイント解説「2.過渡現象におけるコンデンサの過渡状態と定常状態」の通り,定常状態においてはコンデンサは開放として扱えば良い。したがって,定常状態における回路は図1のようになる。
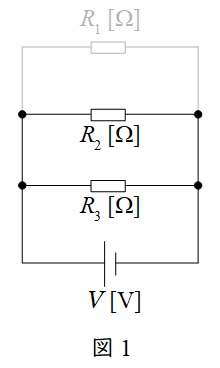
図1より,\( \ R_{2} \ \)と\( \ R_{3} \ \)の並列合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{2}}+\frac {1}{R_{3}} \\[ 5pt ]
R&=&\frac {1}{\displaystyle \frac {1}{R_{2}}+\frac {1}{R_{3}}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,電源を流れる電流\( \ I \ \)は,
\[
\begin{eqnarray}
I&=&\frac {V}{R} \\[ 5pt ]
&=&\frac {V}{\displaystyle \frac {1}{\displaystyle \frac {1}{R_{2}}+\frac {1}{R_{3}}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは